pacman::p_load(rgdal, spdep, tmap, sf,
ggpubr, cluster, factoextra, NbClust,
heatmaply, corrplot, psych, tidyverse,
ClustGeo)Hands-on Exercise 3: Geographical Segmentation with Spatially Constrained Clustering Techniques
1 Overview
In this in-class exercise, we will discuss ClustGeo method for spatially constrained clustering (discussed in Section 9). This is a continuation from the topics discussed in hands-on exercise 3. For easier reading, Sections from hands-on exercise 3 is also added here.
2 Getting Started
2.1 The analytical question
In geobusiness and spatial policy, it is a common practice to delineate the market or planning area into homogeneous regions by using multivariate data. In this exercise, we are interested to delineate Shan State, Myanmar into homogeneous regions by using the penetration of multiple Information and Communication Technology (ICT) measures, namely: Radio, Television, Land line phone, Mobile phone, Computer, and Internet at home.
3 The Data
Two data sets will be used in this study. They are:
Myanmar Township Boundary Data (i.e. myanmar_township_boundaries): This is a GIS data in ESRI shapefile format. It consists of township boundary information of Myanmar. The spatial data are captured in polygon features.
Shan-ICT.csv: This is an extract of The 2014 Myanmar Population and Housing Census Myanmar at the township level.
Both datasets are downloaded from Myanmar Information Management Unit (MIMU)
3.1 Installing and loading R packages
Before we get started, it is important for us to install the necessary R packages into R and launch these R packages into R environment. The R packages needed for this exercise are as follows:
Spatial data handling
- sf, rgdal and spdep
Attribute data handling
- tidyverse (which contains readr, ggplot2 and dplyr)
Choropleth mapping
- tmap
Multivariate data visualisation and analysis
- coorplot, ggpubr, and heatmaply
Cluster analysis
cluster
ClustGeo
The code chunks below installs and launches these R packages into R environment.
4 Data Import and Preparation
4.1 Importing geospatial data into R environment
In this section, we will import Myanmar Township Boundary GIS data and its associated attribute table into R environment.
The Myanmar Township Boundary GIS data is in ERSI shapefile format. It will be imported into R environment by using the st_read() function of sf.
The code chunks used are shown below:
shan_sf <- st_read(dsn = "data/geospatial",
layer = "myanmar_township_boundaries") %>%
filter(ST %in% c("Shan (East)", "Shan (North)", "Shan (South)"))Reading layer `myanmar_township_boundaries' from data source
`C:\lohsiying\ISSS624\in_class_ex\ex3\data\geospatial' using driver `ESRI Shapefile'
Simple feature collection with 330 features and 14 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: 92.17275 ymin: 9.671252 xmax: 101.1699 ymax: 28.54554
Geodetic CRS: WGS 84The imported township boundary object is called shan_sf. It is saved in simple feature data.frame format. We can view the content of the newly created shan_sf simple features data.frame by using the code chunk below.
shan_sfSimple feature collection with 55 features and 14 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: 96.15107 ymin: 19.29932 xmax: 101.1699 ymax: 24.15907
Geodetic CRS: WGS 84
First 10 features:
OBJECTID ST ST_PCODE DT DT_PCODE TS TS_PCODE
1 163 Shan (North) MMR015 Mongmit MMR015D008 Mongmit MMR015017
2 203 Shan (South) MMR014 Taunggyi MMR014D001 Pindaya MMR014006
3 240 Shan (South) MMR014 Taunggyi MMR014D001 Ywangan MMR014007
4 106 Shan (South) MMR014 Taunggyi MMR014D001 Pinlaung MMR014009
5 72 Shan (North) MMR015 Mongmit MMR015D008 Mabein MMR015018
6 40 Shan (South) MMR014 Taunggyi MMR014D001 Kalaw MMR014005
7 194 Shan (South) MMR014 Taunggyi MMR014D001 Pekon MMR014010
8 159 Shan (South) MMR014 Taunggyi MMR014D001 Lawksawk MMR014008
9 61 Shan (North) MMR015 Kyaukme MMR015D003 Nawnghkio MMR015013
10 124 Shan (North) MMR015 Kyaukme MMR015D003 Kyaukme MMR015012
ST_2 LABEL2 SELF_ADMIN ST_RG T_NAME_WIN T_NAME_M3
1 Shan State (North) Mongmit\n61072 <NA> State rdk;rdwf မိုးမိတ်
2 Shan State (South) Pindaya\n77769 Danu State yif;w, ပင်းတယ
3 Shan State (South) Ywangan\n76933 Danu State &GmiH ရွာငံ
4 Shan State (South) Pinlaung\n162537 Pa-O State yifavmif; ပင်လောင်း
5 Shan State (North) Mabein\n35718 <NA> State rbdrf; မဘိမ်း
6 Shan State (South) Kalaw\n163138 <NA> State uavm ကလော
7 Shan State (South) Pekon\n94226 <NA> State z,fcHk ဖယ်ခုံ
8 Shan State (South) Lawksawk <NA> State &yfapmuf ရပ်စောက်
9 Shan State (North) Nawnghkio\n128357 <NA> State aemifcsdK နောင်ချို
10 Shan State (North) Kyaukme\n172874 <NA> State ausmufrJ ကျောက်မဲ
AREA geometry
1 2703.611 MULTIPOLYGON (((96.96001 23...
2 629.025 MULTIPOLYGON (((96.7731 21....
3 2984.377 MULTIPOLYGON (((96.78483 21...
4 3396.963 MULTIPOLYGON (((96.49518 20...
5 5034.413 MULTIPOLYGON (((96.66306 24...
6 1456.624 MULTIPOLYGON (((96.49518 20...
7 2073.513 MULTIPOLYGON (((97.14738 19...
8 5145.659 MULTIPOLYGON (((96.94981 22...
9 3271.537 MULTIPOLYGON (((96.75648 22...
10 3920.869 MULTIPOLYGON (((96.95498 22...Since sf.data.frame conforms to the tidy framework, we can use glimpse()` to reveal the data type in each field in shan_sf.
4.2 Importing aspatial data into R environment
The csv file will be imported using read_csv frunction of readr package as shown in the following code chunk:
ict <- read_csv ("data/aspatial/Shan-ICT.csv")The imported InfoComm variables are extracted from The 2014 Myanmar Population and Housing Census Myanmar. The attribute data set is called ict. It is saved in R’s tibble data.frame format.
The code chunk below shows the summary statistics of ict data.frame.
summary(ict) District Pcode District Name Township Pcode Township Name
Length:55 Length:55 Length:55 Length:55
Class :character Class :character Class :character Class :character
Mode :character Mode :character Mode :character Mode :character
Total households Radio Television Land line phone
Min. : 3318 Min. : 115 Min. : 728 Min. : 20.0
1st Qu.: 8711 1st Qu.: 1260 1st Qu.: 3744 1st Qu.: 266.5
Median :13685 Median : 2497 Median : 6117 Median : 695.0
Mean :18369 Mean : 4487 Mean :10183 Mean : 929.9
3rd Qu.:23471 3rd Qu.: 6192 3rd Qu.:13906 3rd Qu.:1082.5
Max. :82604 Max. :30176 Max. :62388 Max. :6736.0
Mobile phone Computer Internet at home
Min. : 150 Min. : 20.0 Min. : 8.0
1st Qu.: 2037 1st Qu.: 121.0 1st Qu.: 88.0
Median : 3559 Median : 244.0 Median : 316.0
Mean : 6470 Mean : 575.5 Mean : 760.2
3rd Qu.: 7177 3rd Qu.: 507.0 3rd Qu.: 630.5
Max. :48461 Max. :6705.0 Max. :9746.0 We can see that there a total of eleven fields and 55 observations in the tibble data.frame.
4.3 Deriving new variables using dplyr package
The data in ict provides the count of the number of households. Such units of measurement is directly biased by the underlying total number of households in the town. In general, the townships with relatively higher total number of households will also have higher number of households owning radio, TV etc.
In order to overcome this issue, we will derive the penetration rate for each ICT by using the code chunk below. We will multiply by 1000 so that we have the statistics for per thousand household.
ict_derived <- ict %>%
mutate(`RADIO_PR` = `Radio`/`Total households`*1000) %>%
mutate(`TV_PR` = `Television`/`Total households`*1000) %>%
mutate(`LLPHONE_PR` = `Land line phone`/`Total households`*1000) %>%
mutate(`MPHONE_PR` = `Mobile phone`/`Total households`*1000) %>%
mutate(`COMPUTER_PR` = `Computer`/`Total households`*1000) %>%
mutate(`INTERNET_PR` = `Internet at home`/`Total households`*1000) %>%
rename(`DT_PCODE` =`District Pcode`,
`DT`=`District Name`,
`TS_PCODE`=`Township Pcode`,
`TS`=`Township Name`,
`TT_HOUSEHOLDS`=`Total households`,
`RADIO`=`Radio`,
`TV`=`Television`,
`LLPHONE`=`Land line phone`,
`MPHONE`=`Mobile phone`,
`COMPUTER`=`Computer`,
`INTERNET`=`Internet at home`) We can review the summary statistics of the newly derived variables using the code chunk below.
summary(ict_derived) DT_PCODE DT TS_PCODE TS
Length:55 Length:55 Length:55 Length:55
Class :character Class :character Class :character Class :character
Mode :character Mode :character Mode :character Mode :character
TT_HOUSEHOLDS RADIO TV LLPHONE
Min. : 3318 Min. : 115 Min. : 728 Min. : 20.0
1st Qu.: 8711 1st Qu.: 1260 1st Qu.: 3744 1st Qu.: 266.5
Median :13685 Median : 2497 Median : 6117 Median : 695.0
Mean :18369 Mean : 4487 Mean :10183 Mean : 929.9
3rd Qu.:23471 3rd Qu.: 6192 3rd Qu.:13906 3rd Qu.:1082.5
Max. :82604 Max. :30176 Max. :62388 Max. :6736.0
MPHONE COMPUTER INTERNET RADIO_PR
Min. : 150 Min. : 20.0 Min. : 8.0 Min. : 21.05
1st Qu.: 2037 1st Qu.: 121.0 1st Qu.: 88.0 1st Qu.:138.95
Median : 3559 Median : 244.0 Median : 316.0 Median :210.95
Mean : 6470 Mean : 575.5 Mean : 760.2 Mean :215.68
3rd Qu.: 7177 3rd Qu.: 507.0 3rd Qu.: 630.5 3rd Qu.:268.07
Max. :48461 Max. :6705.0 Max. :9746.0 Max. :484.52
TV_PR LLPHONE_PR MPHONE_PR COMPUTER_PR
Min. :116.0 Min. : 2.78 Min. : 36.42 Min. : 3.278
1st Qu.:450.2 1st Qu.: 22.84 1st Qu.:190.14 1st Qu.:11.832
Median :517.2 Median : 37.59 Median :305.27 Median :18.970
Mean :509.5 Mean : 51.09 Mean :314.05 Mean :24.393
3rd Qu.:606.4 3rd Qu.: 69.72 3rd Qu.:428.43 3rd Qu.:29.897
Max. :842.5 Max. :181.49 Max. :735.43 Max. :92.402
INTERNET_PR
Min. : 1.041
1st Qu.: 8.617
Median : 22.829
Mean : 30.644
3rd Qu.: 41.281
Max. :117.985 5 Exploratory Data Analysis (EDA)
5.1 EDA using statistical graphs
We can plot the overall distribution of the variables by using a histogram. Using a histogram allows us to identify the overall distribution of the data values (i.e. left skew, right skew or normal distribution).
In the following code chunk, we derive the histogram plot for the number of radios.
ggplot(data=ict_derived,
aes(x=`RADIO`)) +
geom_histogram(bins=20,
color="black",
fill="light blue")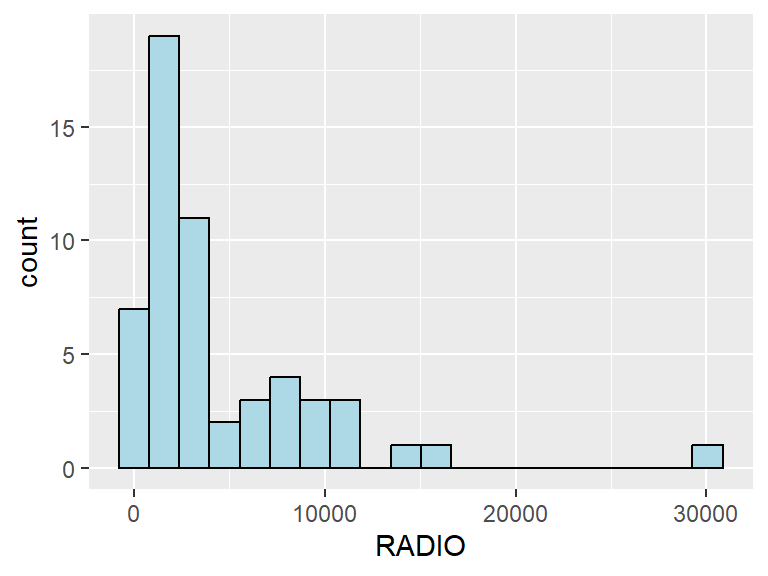
To identify outliers, boxplots can be used.
ggplot(data=ict_derived,
aes(x=`RADIO`)) +
geom_boxplot(color="black",
fill="light blue")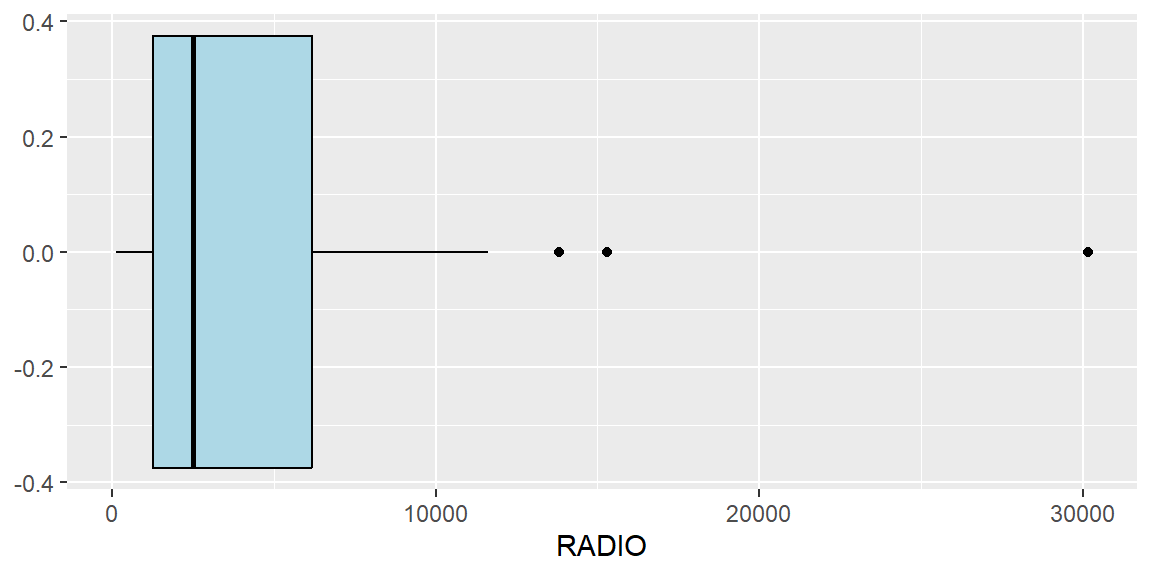
Next, we will plot the distribution of the newly derived variables. In the following code chunk, we plot the histogram for the radio penetration rate.
ggplot(data=ict_derived,
aes(x=`RADIO_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue")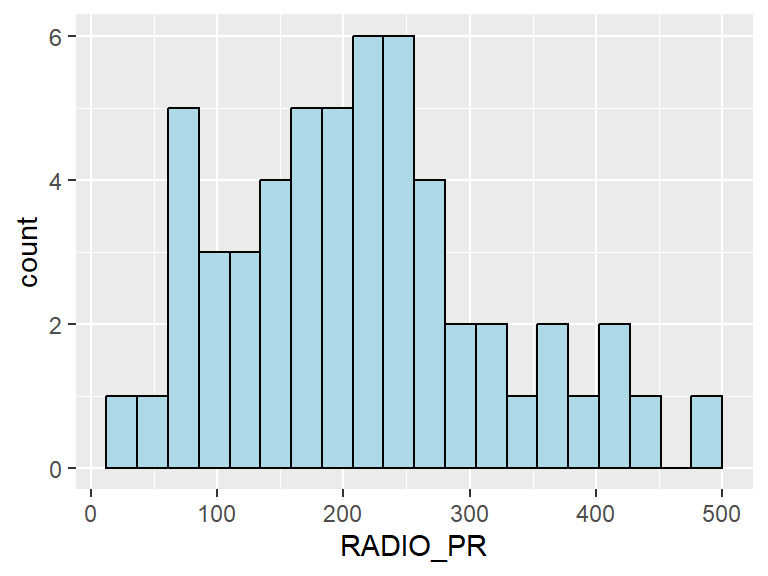
From the histogram, we can observe a slight right skew in the distribution of the radio penetration rate - there is more lower radio pentration rates compared to higher radio penetration rates.
Likewise, we will generate the boxplot for the radio pentration rate.
ggplot(data=ict_derived,
aes(x=`RADIO_PR`)) +
geom_boxplot(color="black",
fill="light blue")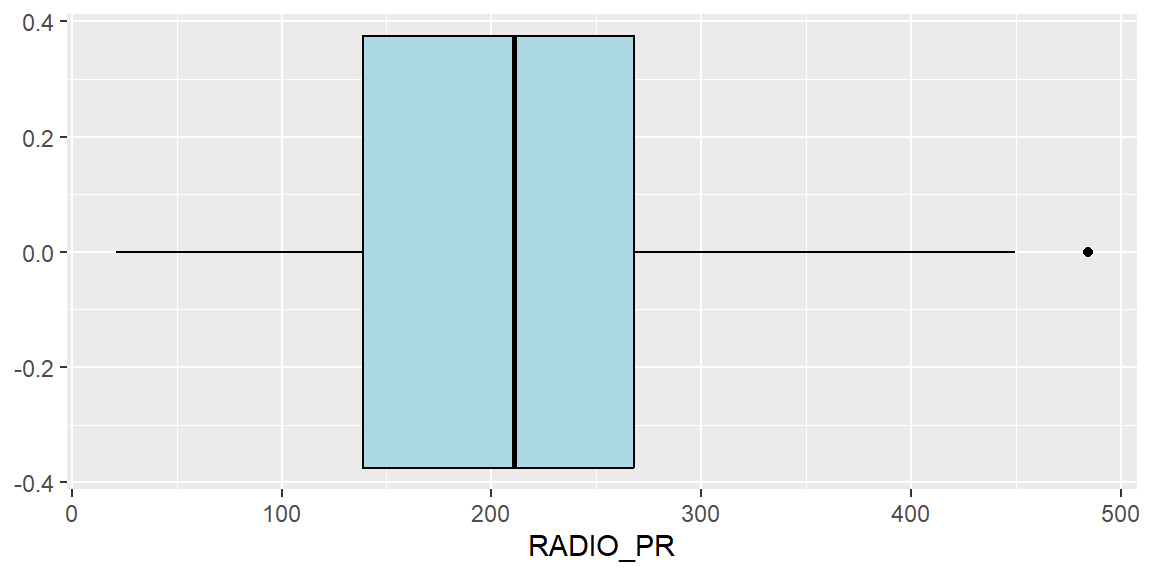
From the boxplot, we can see that the median radio pentration rate is slightly over 20%. It can also be observed that there is an outlier township that with significantly high radio penetration rate of about 49%. The range of radio pentration rate across the townships also vary widely, from about 2% to 49% penetration rates.
We can also plot multiple histograms together in the same plot to reveal the distribution of various variables. We can do this by first creating the individual histograms and then using ggarange() function from ggpubr package is used to group these histograms together.
radio <- ggplot(data=ict_derived,
aes(x= `RADIO_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue")
tv <- ggplot(data=ict_derived,
aes(x= `TV_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue")
llphone <- ggplot(data=ict_derived,
aes(x= `LLPHONE_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue")
mphone <- ggplot(data=ict_derived,
aes(x= `MPHONE_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue")
computer <- ggplot(data=ict_derived,
aes(x= `COMPUTER_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue")
internet <- ggplot(data=ict_derived,
aes(x= `INTERNET_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue")
ggarrange(radio, tv, llphone, mphone, computer, internet,
ncol = 3,
nrow = 2)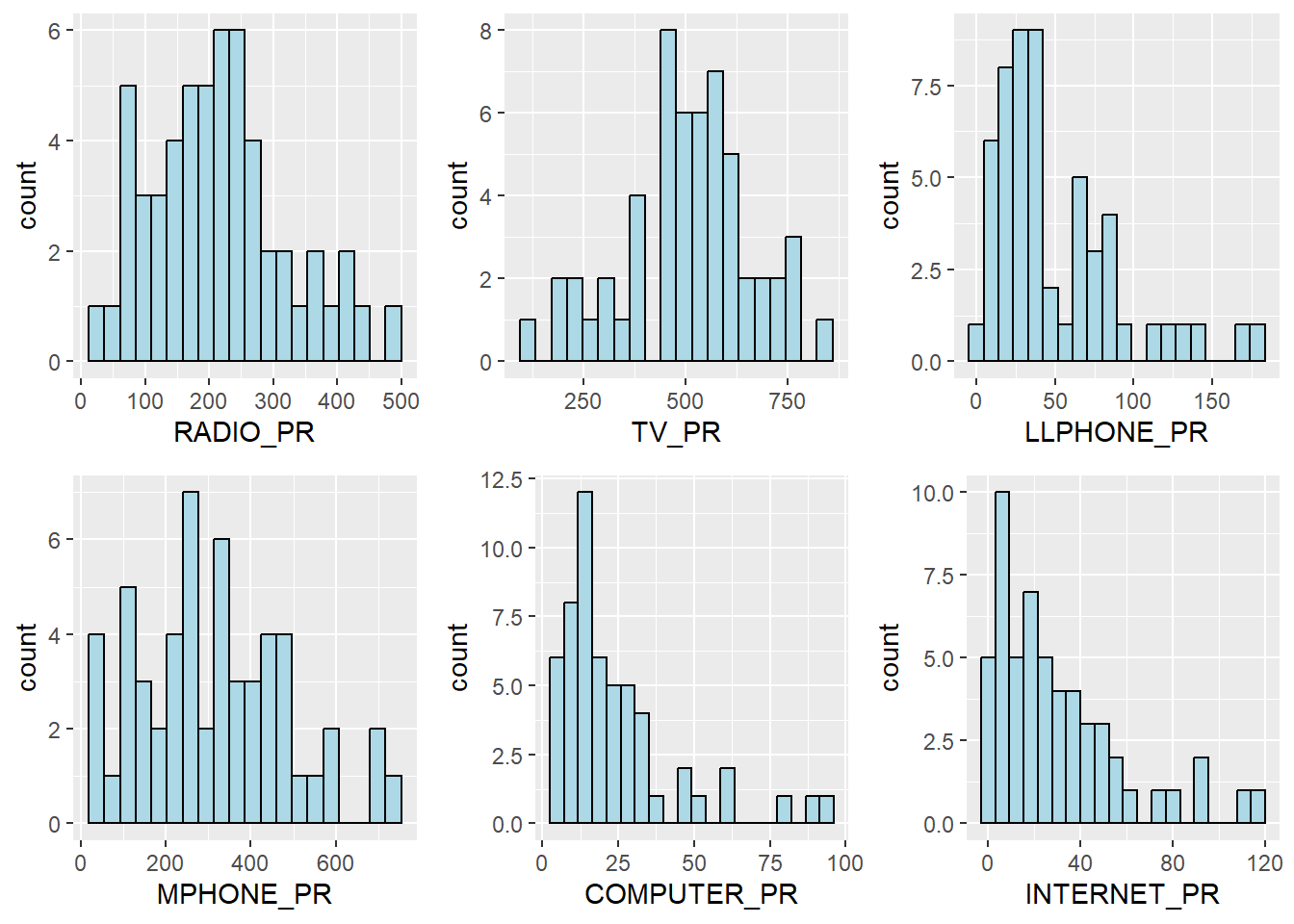
5.2 EDA using choropleth map
5.2.1 Joining geospatial data with aspatial data
In order to plot the choropleth map, we need to combine the geospatial data object (i.e. shan_sf) and aspatial data.frame object (i.e. ict_derived). This will be performed by using the left_join function of dplyr package. The shan_sf simple feature data.frame will be used as the base data object and the ict_derived data.frame will be used as the join table to keep the geometry field in shan_sf.
The code chunks below is used to perform the task. The unique identifier used to join both data objects is TS_PCODE.
shan_sf <- left_join(shan_sf,
ict_derived,
by=c("TS_PCODE"="TS_PCODE"))5.2.2 Plotting a choropleth map
We will have a look at the distribution of Radio penetration rate of Shan State at township level by plotting a choropleth map. The code chunks below are used to prepare the choroplethby using the qtm() function of tmap package.
qtm(shan_sf, "RADIO_PR")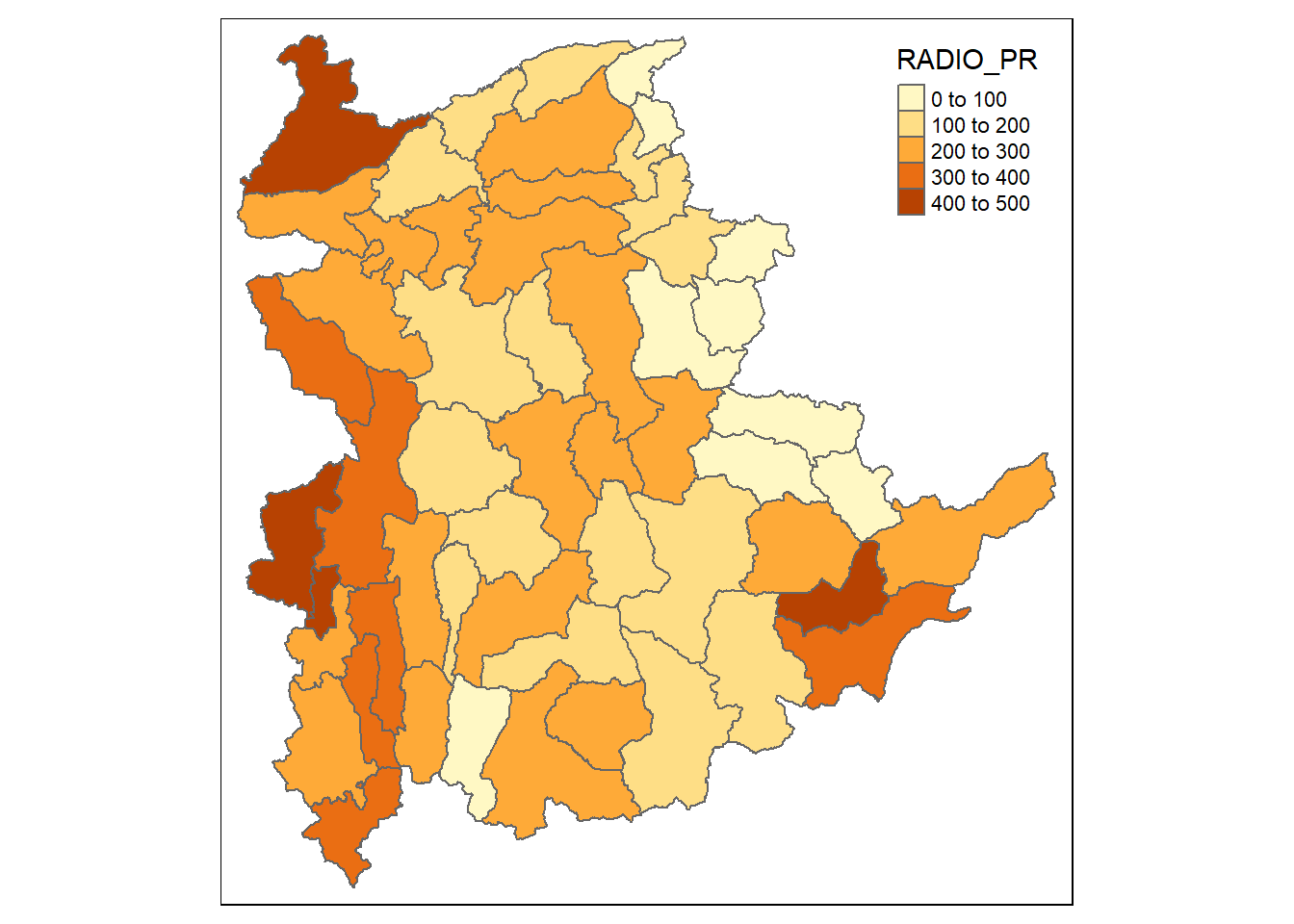
However, the distribution shown in the choropleth map above are bias to the underlying total number of households at the townships. To demonstrate this, we will create two choropleth maps, one for the total number of households (i.e. TT_HOUSEHOLDS.map) and one for the total number of household with Radio (RADIO.map) by using the code chunk below.
TT_HOUSEHOLDS.map <- tm_shape(shan_sf) +
tm_fill(col = "TT_HOUSEHOLDS",
n = 5,
style = "jenks",
title = "Total households") +
tm_borders(alpha = 0.5)
RADIO.map <- tm_shape(shan_sf) +
tm_fill(col = "RADIO",
n = 5,
style = "jenks",
title = "Number Radio ") +
tm_borders(alpha = 0.5)
tmap_arrange(TT_HOUSEHOLDS.map, RADIO.map,
asp=NA, ncol=2)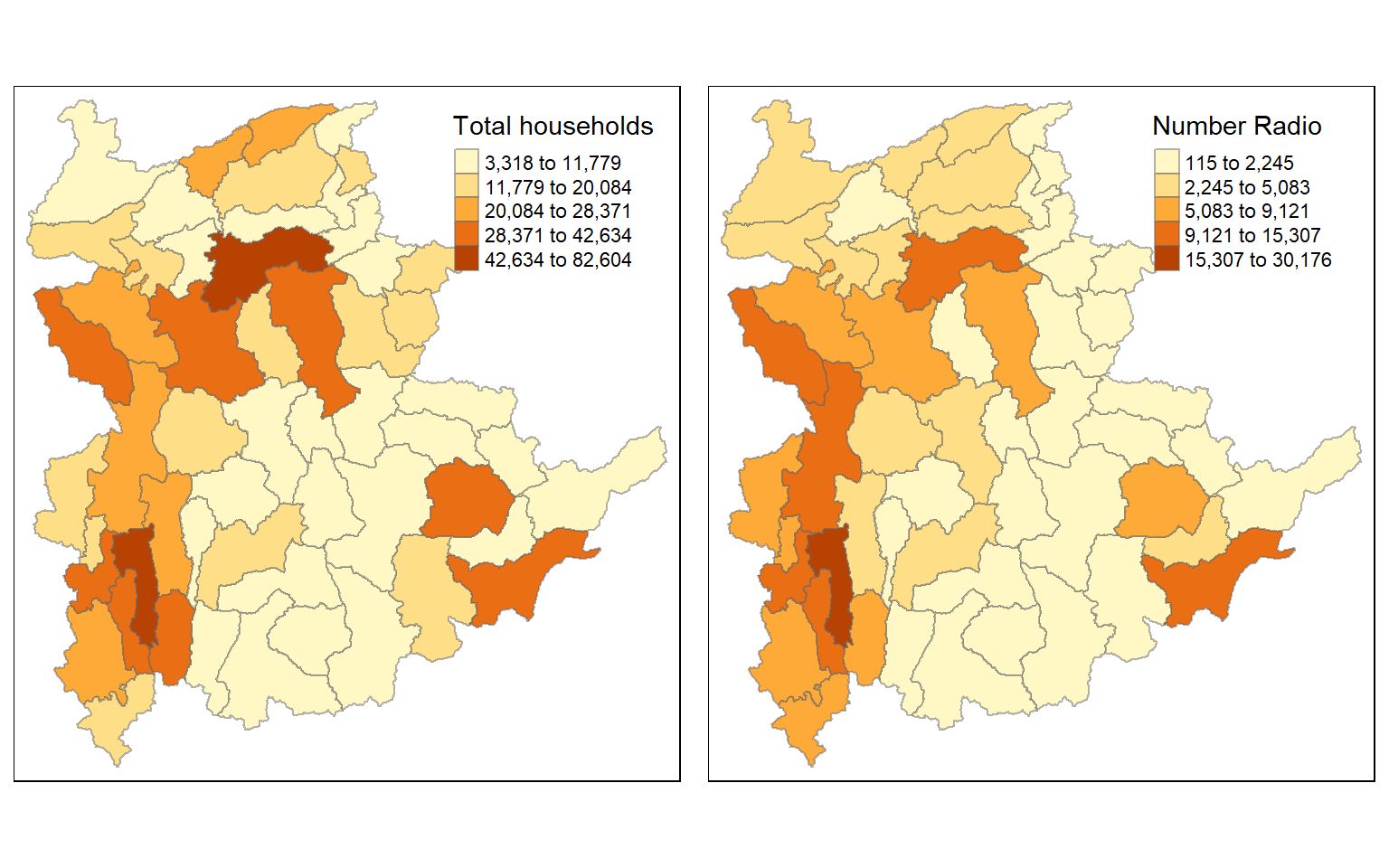
The choropleth maps above clearly show that townships with relatively larger number ot households are also showing relatively higher number of radio ownership.
Now let us plot the choropleth maps showing the distribution of total number of households and Radio penetration rate by using the code chunk below.
tm_shape(shan_sf) +
tm_polygons(c("TT_HOUSEHOLDS", "RADIO_PR"),
style="jenks") +
tm_facets(sync = TRUE, ncol = 2) +
tm_legend(legend.position = c("right", "bottom"))+
tm_layout(outer.margins=0, asp=0)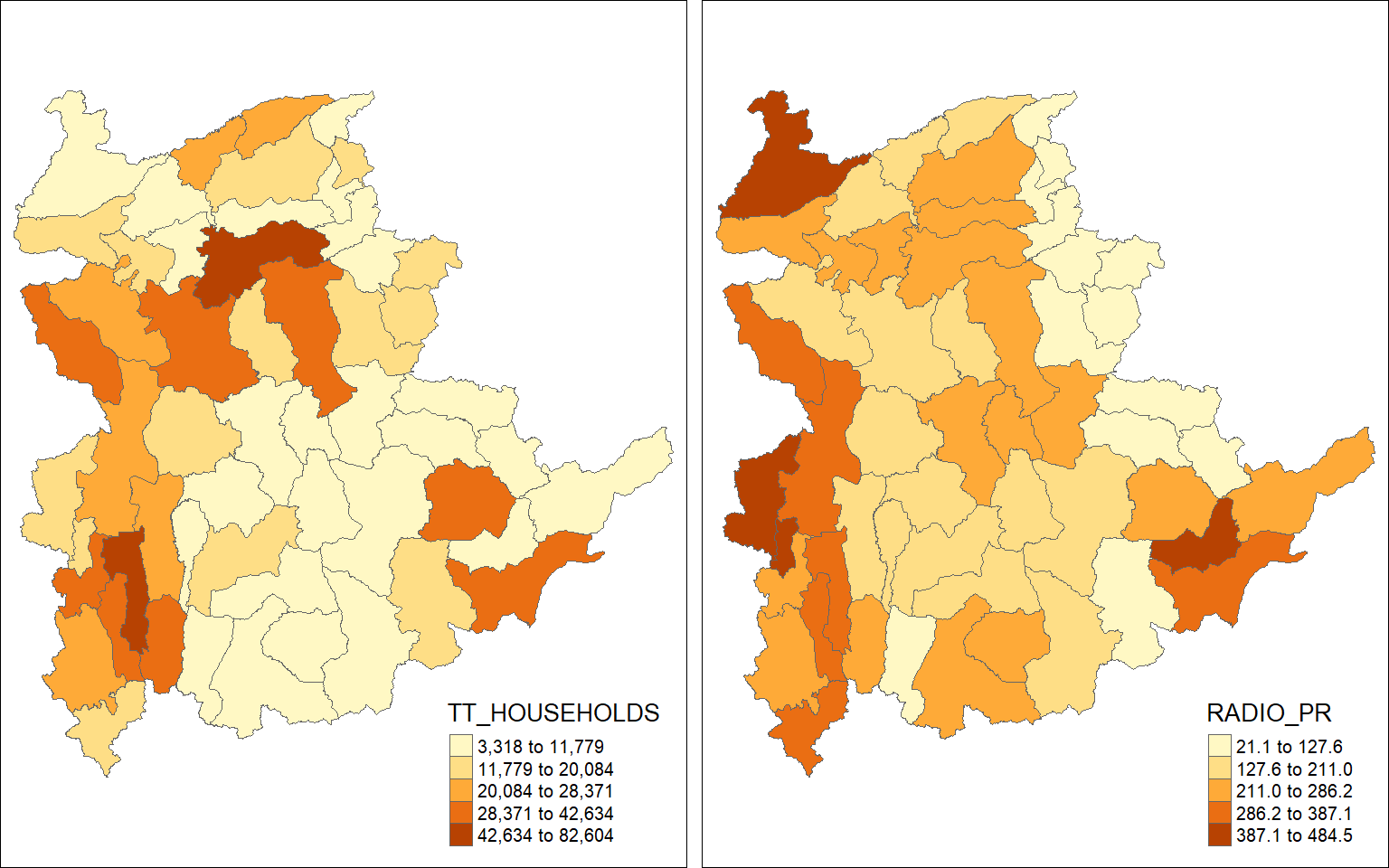
Here, we can see that larger townships do not necessarily have higher radio penetration. By using the radio penetration rate, we are able to correctly reflect which township has higher proportion of their residents having radios.
6 Correlation Analysis
It is important for us to ensure that cluster variables are not highly correlated when we perform cluster analysis. This is because we do not want to give extra weight to these highly correlated variables.
We will use corrplot.mixed() function of corrplot package to visualise and analyse the correlation between the input variables.
cluster_vars.cor = cor(ict_derived[,12:17])
corrplot.mixed(cluster_vars.cor,
lower = "ellipse",
upper = "number",
tl.pos = "lt",
diag = "l",
tl.col = "black")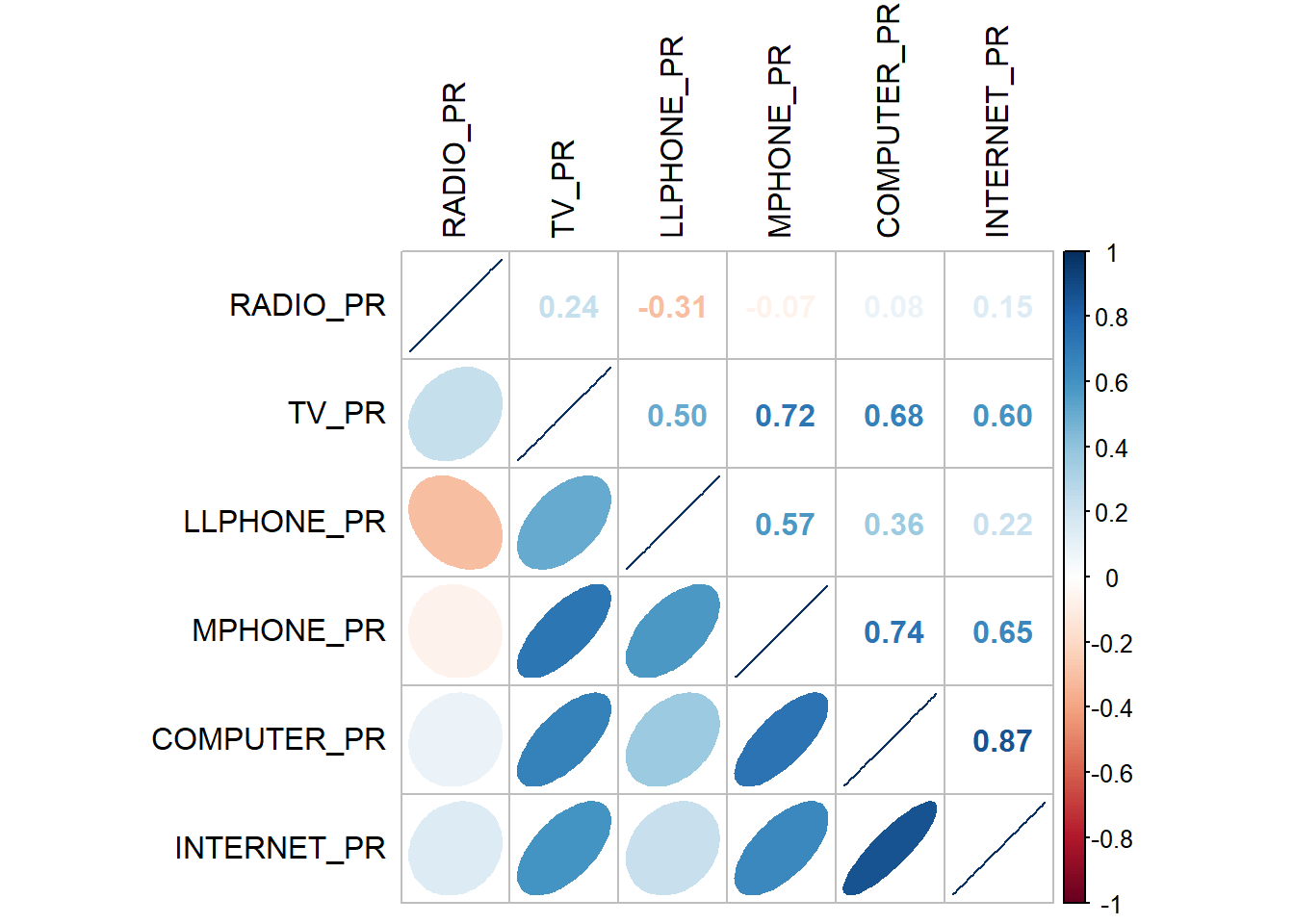
The fatter the ellipse, the more weakly correlated they are. Moving more like a line, means more strongly correlated.
The correlation plot above shows that COMPUTER_PR and INTERNET_PR are highly correlated. This suggest that only one of them should be used in the cluster analysis.
7 Hierarchical Cluster Analysis
In this section, we will perform hierarchical cluster analysis.
7.1 Extracting clustering variables
The code chunk below will be used to extract the clustering variables from the shan_sf simple feature object into a data.frame. We will exclude the variables INTERNET_PR and keep only the COMPUTER_PR. We will also remove the geometry field by setting it to null (we will not be able to exclude the geometry column by using select()).
cluster_vars <- shan_sf %>%
st_set_geometry(NULL) %>%
select("TS.x", "RADIO_PR", "TV_PR", "LLPHONE_PR", "MPHONE_PR", "COMPUTER_PR")
head(cluster_vars,10) TS.x RADIO_PR TV_PR LLPHONE_PR MPHONE_PR COMPUTER_PR
1 Mongmit 286.1852 554.1313 35.30618 260.6944 12.15939
2 Pindaya 417.4647 505.1300 19.83584 162.3917 12.88190
3 Ywangan 484.5215 260.5734 11.93591 120.2856 4.41465
4 Pinlaung 231.6499 541.7189 28.54454 249.4903 13.76255
5 Mabein 449.4903 708.6423 72.75255 392.6089 16.45042
6 Kalaw 280.7624 611.6204 42.06478 408.7951 29.63160
7 Pekon 318.6118 535.8494 39.83270 214.8476 18.97032
8 Lawksawk 387.1017 630.0035 31.51366 320.5686 21.76677
9 Nawnghkio 349.3359 547.9456 38.44960 323.0201 15.76465
10 Kyaukme 210.9548 601.1773 39.58267 372.4930 30.94709Next, we will use the township name as the row names instead of using row number.
row.names(cluster_vars) <- cluster_vars$"TS.x"
head(cluster_vars,10) TS.x RADIO_PR TV_PR LLPHONE_PR MPHONE_PR COMPUTER_PR
Mongmit Mongmit 286.1852 554.1313 35.30618 260.6944 12.15939
Pindaya Pindaya 417.4647 505.1300 19.83584 162.3917 12.88190
Ywangan Ywangan 484.5215 260.5734 11.93591 120.2856 4.41465
Pinlaung Pinlaung 231.6499 541.7189 28.54454 249.4903 13.76255
Mabein Mabein 449.4903 708.6423 72.75255 392.6089 16.45042
Kalaw Kalaw 280.7624 611.6204 42.06478 408.7951 29.63160
Pekon Pekon 318.6118 535.8494 39.83270 214.8476 18.97032
Lawksawk Lawksawk 387.1017 630.0035 31.51366 320.5686 21.76677
Nawnghkio Nawnghkio 349.3359 547.9456 38.44960 323.0201 15.76465
Kyaukme Kyaukme 210.9548 601.1773 39.58267 372.4930 30.94709We can then delete the TS.x field (column for township names).
shan_ict <- select(cluster_vars, c(2:6))
head(shan_ict, 10) RADIO_PR TV_PR LLPHONE_PR MPHONE_PR COMPUTER_PR
Mongmit 286.1852 554.1313 35.30618 260.6944 12.15939
Pindaya 417.4647 505.1300 19.83584 162.3917 12.88190
Ywangan 484.5215 260.5734 11.93591 120.2856 4.41465
Pinlaung 231.6499 541.7189 28.54454 249.4903 13.76255
Mabein 449.4903 708.6423 72.75255 392.6089 16.45042
Kalaw 280.7624 611.6204 42.06478 408.7951 29.63160
Pekon 318.6118 535.8494 39.83270 214.8476 18.97032
Lawksawk 387.1017 630.0035 31.51366 320.5686 21.76677
Nawnghkio 349.3359 547.9456 38.44960 323.0201 15.76465
Kyaukme 210.9548 601.1773 39.58267 372.4930 30.94709Now that our data.frame only contains clustering variables as attributes, we can perform clustering using this data.frame. The township names are in the row index and will not be used as variables for clustering. Also, when we plot the dendrogram, the township names will be the leaves.
7.2 Data Standardisation
Next, we will perform data standardisation. It is not unusual that value ranges of differnet variables can differ significantly. As we want to avoid the cluster analysis from being biased towards clustering variables that have larger values.
7.2.1 Min-Max standardisation
In the code chunk below, normalize() of heatmaply package is used to stadardisation the clustering variables by using Min-Max method. The summary() is then used to display the summary statistics of the standardised clustering variables.
shan_ict.std <- normalize(shan_ict)
summary(shan_ict.std) RADIO_PR TV_PR LLPHONE_PR MPHONE_PR
Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. :0.0000
1st Qu.:0.2544 1st Qu.:0.4600 1st Qu.:0.1123 1st Qu.:0.2199
Median :0.4097 Median :0.5523 Median :0.1948 Median :0.3846
Mean :0.4199 Mean :0.5416 Mean :0.2703 Mean :0.3972
3rd Qu.:0.5330 3rd Qu.:0.6750 3rd Qu.:0.3746 3rd Qu.:0.5608
Max. :1.0000 Max. :1.0000 Max. :1.0000 Max. :1.0000
COMPUTER_PR
Min. :0.00000
1st Qu.:0.09598
Median :0.17607
Mean :0.23692
3rd Qu.:0.29868
Max. :1.00000 We can observe that the value range for each variable is now between 0 and 1 after min0max standardisation is performed.
7.2.2 Z-score standardisation
Z-score standardisation can be performed by using scale() of Base R. The code chunk below will be used to stadardisation the clustering variables by using Z-score method. In here, we will use describe() from psych package to to review the results instead of summary() of Base R because the describe() provides standard deviation.
shan_ict.z <- scale(shan_ict)
describe(shan_ict.z) vars n mean sd median trimmed mad min max range skew kurtosis
RADIO_PR 1 55 0 1 -0.04 -0.06 0.94 -1.85 2.55 4.40 0.48 -0.27
TV_PR 2 55 0 1 0.05 0.04 0.78 -2.47 2.09 4.56 -0.38 -0.23
LLPHONE_PR 3 55 0 1 -0.33 -0.15 0.68 -1.19 3.20 4.39 1.37 1.49
MPHONE_PR 4 55 0 1 -0.05 -0.06 1.01 -1.58 2.40 3.98 0.48 -0.34
COMPUTER_PR 5 55 0 1 -0.26 -0.18 0.64 -1.03 3.31 4.34 1.80 2.96
se
RADIO_PR 0.13
TV_PR 0.13
LLPHONE_PR 0.13
MPHONE_PR 0.13
COMPUTER_PR 0.13We can observe that the mean and standard deviation of the Z-score standardised variable are now 0 and 1 respectively. However, we will also need to wary that Z-score standardisation method should only be used if we would assume all variables come from some normal distribution.
7.2.3 Visualising the standardised clustering variables
Beside reviewing the summary statistics of the standardised clustering variables, it is also a good practice to visualise their distribution graphical.
The code chunk below plots the scaled Radio_PR field.
r <- ggplot(data=ict_derived,
aes(x= `RADIO_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue")
shan_ict_s_df <- as.data.frame(shan_ict.std)
s <- ggplot(data=shan_ict_s_df,
aes(x=`RADIO_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue") +
ggtitle("Min-Max Standardisation")
shan_ict_z_df <- as.data.frame(shan_ict.z)
z <- ggplot(data=shan_ict_z_df,
aes(x=`RADIO_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue") +
ggtitle("Z-score Standardisation")
ggarrange(r, s, z,
ncol = 3,
nrow = 1)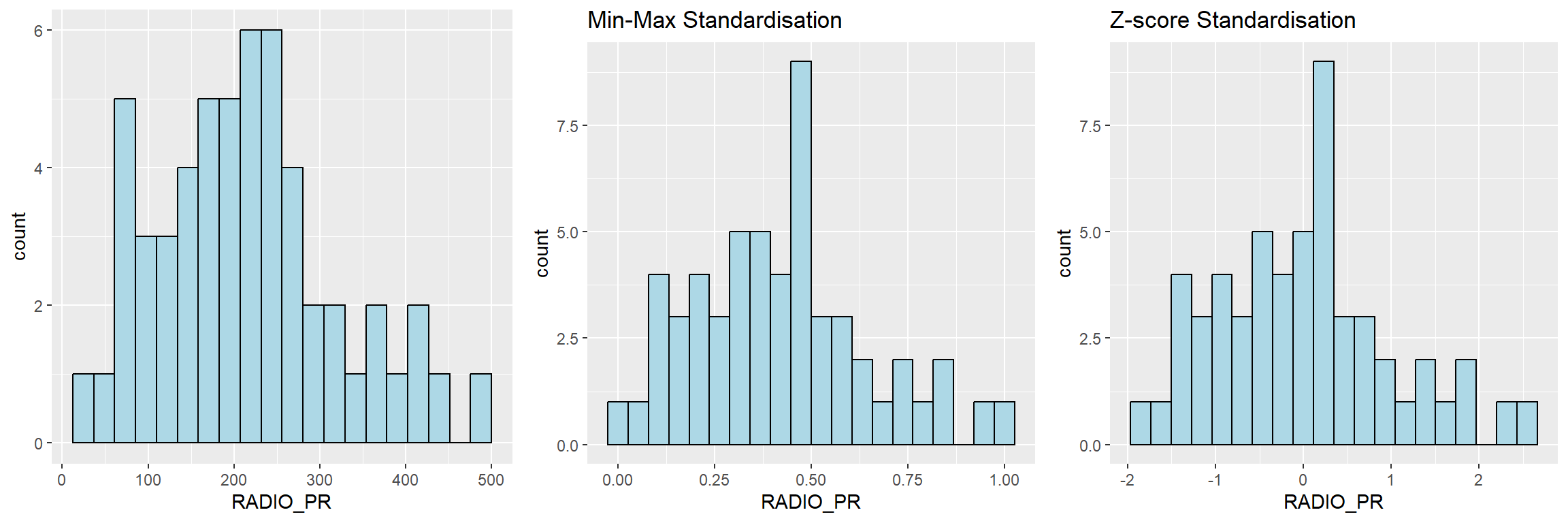
We can observe that the overall distribution of the clustering variable changes after data standardisation is performed. Hence, it is not advisable to perform data standardisation if the value ranges of the clustering variables are not very large.
7.3 Computing proximity matrix
In R, there are many packages that provide functions to calculate distance matrix. We will compute the proximity matrix by using dist() of R.
dist() supports six distance proximity calculations: euclidean, maximum, manhattan, canberra, binary and minkowski. The default is the euclidean proximity matrix.
The code chunk below is used to compute the proximity matrix using euclidean method.
proxmat <- dist(shan_ict, method = 'euclidean')7.4 Computing hierarchical clustering
In R, there are several packages provide hierarchical clustering function. In this hands-on exercise, hclust() of R stats will be used. There are eight clustering algorithms are supported, they are: ward.D, ward.D2, single, complete, average(UPGMA), mcquitty(WPGMA), median(WPGMC) and centroid(UPGMC).
The code chunk below performs hierarchical cluster analysis using ward.D method. The hierarchical clustering output is stored in an object of class hclust which describes the dendrogram produced by the clustering process.
hclust_ward <- hclust(proxmat, method = 'ward.D')We can then plot the dendrogram by using plot() of R Graphics as shown in the code chunk below.
plot(hclust_ward, cex = 0.6)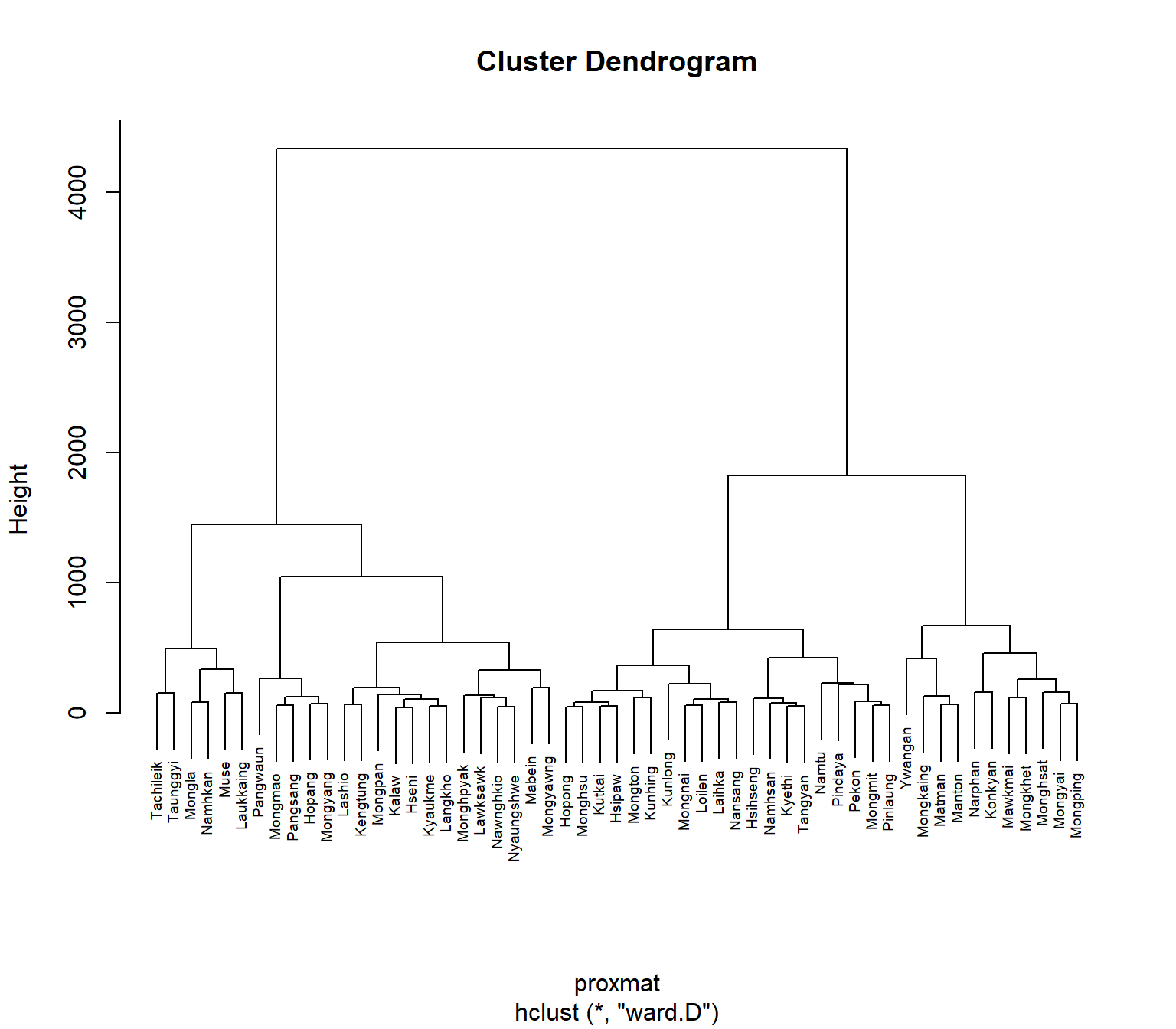
7.5 Selecting the optimal clustering algorithm
One of the challenges in performing hierarchical clustering is to identify the strongest clustering structures. The issue can be solved by using agnes() function from cluster package. It functions like hclus(), however, with the agnes() function we can also get the agglomerative coefficient, which measures the amount of clustering structure found. The closer the coefficient is to 1, the stronger the clustering structure.
The code chunk below will be used to compute the agglomerative coefficients of 4 hierarchical clustering algorithm: “average”, “single”, “complete”, and “ward”.
m <- c( "average", "single", "complete", "ward")
names(m) <- c( "average", "single", "complete", "ward")
ac <- function(x) {
agnes(shan_ict, method = x)$ac
}
map_dbl(m, ac) average single complete ward
0.8131144 0.6628705 0.8950702 0.9427730 We can see that Ward’s method provides the strongest clustering structure among the four methods assessed. Hence, in the subsequent analysis, only Ward’s method will be used.
7.6 Determining the optimal number of clusters
Another technical challenge face by data analyst in performing clustering analysis is to determine the optimal clusters to retain.
There are three commonly used methods to determine the optimal clusters, they are:
Here, we will explore the gap statistic method.
7.6.1 Gap statistic method
The gap statistic compares the total intra-cluster variation for different values of k with their expected values under null reference distribution of the data. The estimate of the optimal clusters will be the value that maximizes the gap statistic (i.e., that yields the largest gap statistic). This means that the clustering structure is furthest away from the random uniform distribution of points.
To compute the gap statistic, clusGap() of cluster package will be used.
set.seed(12345)
gap_stat <- clusGap(shan_ict,
FUN = hcut,
nstart = 25,
K.max = 10,
B = 50)
# Print the result
print(gap_stat, method = "firstmax")Clustering Gap statistic ["clusGap"] from call:
clusGap(x = shan_ict, FUNcluster = hcut, K.max = 10, B = 50, nstart = 25)
B=50 simulated reference sets, k = 1..10; spaceH0="scaledPCA"
--> Number of clusters (method 'firstmax'): 1
logW E.logW gap SE.sim
[1,] 8.407129 8.680794 0.2736651 0.04460994
[2,] 8.130029 8.350712 0.2206824 0.03880130
[3,] 7.992265 8.202550 0.2102844 0.03362652
[4,] 7.862224 8.080655 0.2184311 0.03784781
[5,] 7.756461 7.978022 0.2215615 0.03897071
[6,] 7.665594 7.887777 0.2221833 0.03973087
[7,] 7.590919 7.806333 0.2154145 0.04054939
[8,] 7.526680 7.731619 0.2049390 0.04198644
[9,] 7.458024 7.660795 0.2027705 0.04421874
[10,] 7.377412 7.593858 0.2164465 0.04540947Next, we can visualise the plot by using fviz_gap_stat() of factoextra package.
fviz_gap_stat(gap_stat)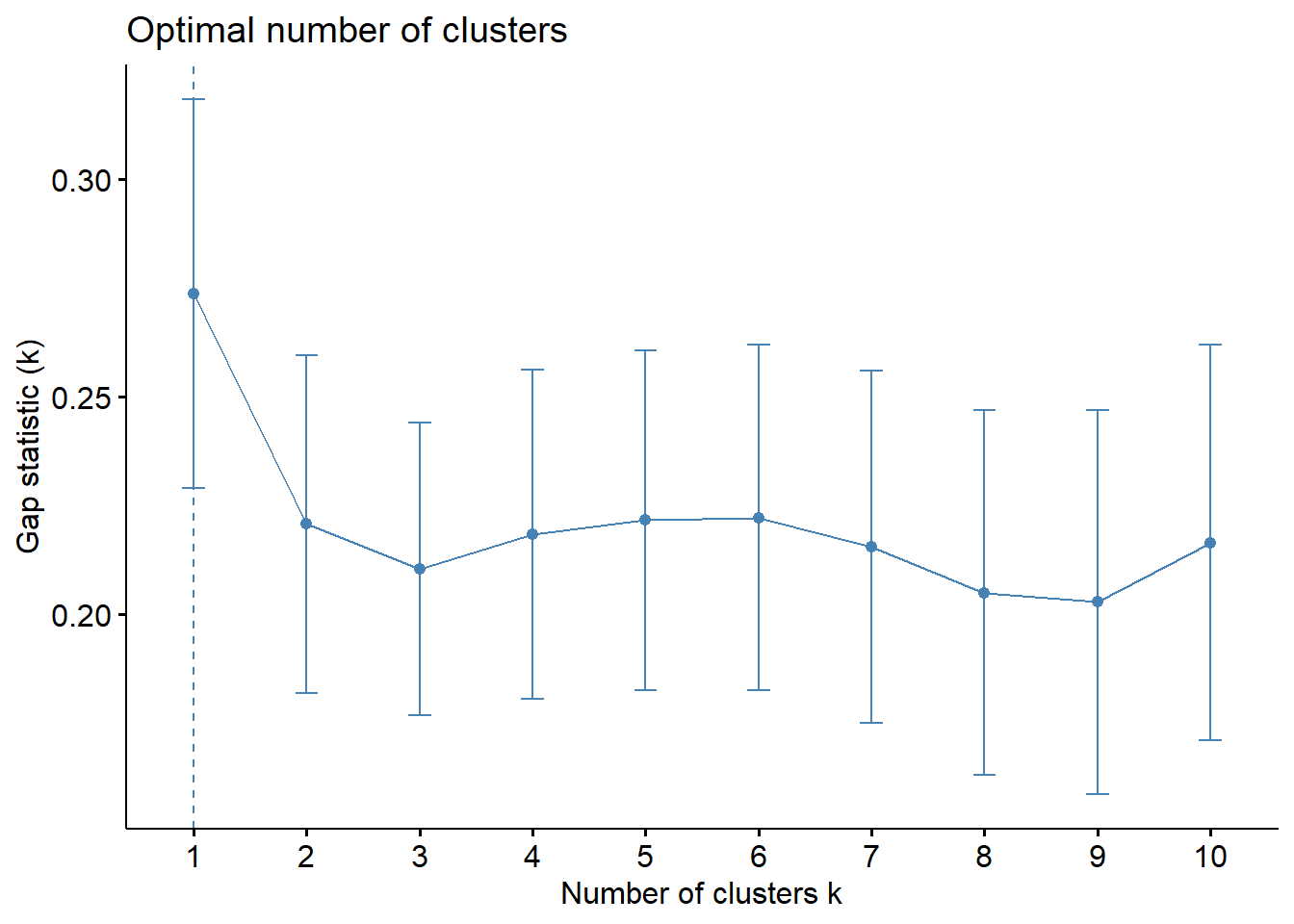
With reference to the gap statistic graph above, the recommended number of cluster to retain is 1. However, it is not logical to retain only one cluster. By examine the gap statistic graph, the 6-cluster gives the next largest gap statistic and should be the next best cluster to pick.
7.7 Interpreting the dendrograms
In the dendrogram displayed above, each leaf corresponds to one observation. As we move up the tree, observations that are similar to each other are combined into branches, which are themselves fused at a higher height.
We use the height of the fusion, provided on the vertical axis, to tell the (dis)similarity between two observations. The higher the height of the fusion, the less similar the observations are. Such conclusions on proximity of two observations can only be drawn based on the height where the branches containing those two observations first are fused.
It’s also possible to draw the dendrogram with a border around the selected clusters by using rect.hclust() of R stats. The argument border is used to specify the border colors for the rectangles.
plot(hclust_ward, cex = 0.6)
rect.hclust(hclust_ward,
k = 6,
border = 2:5)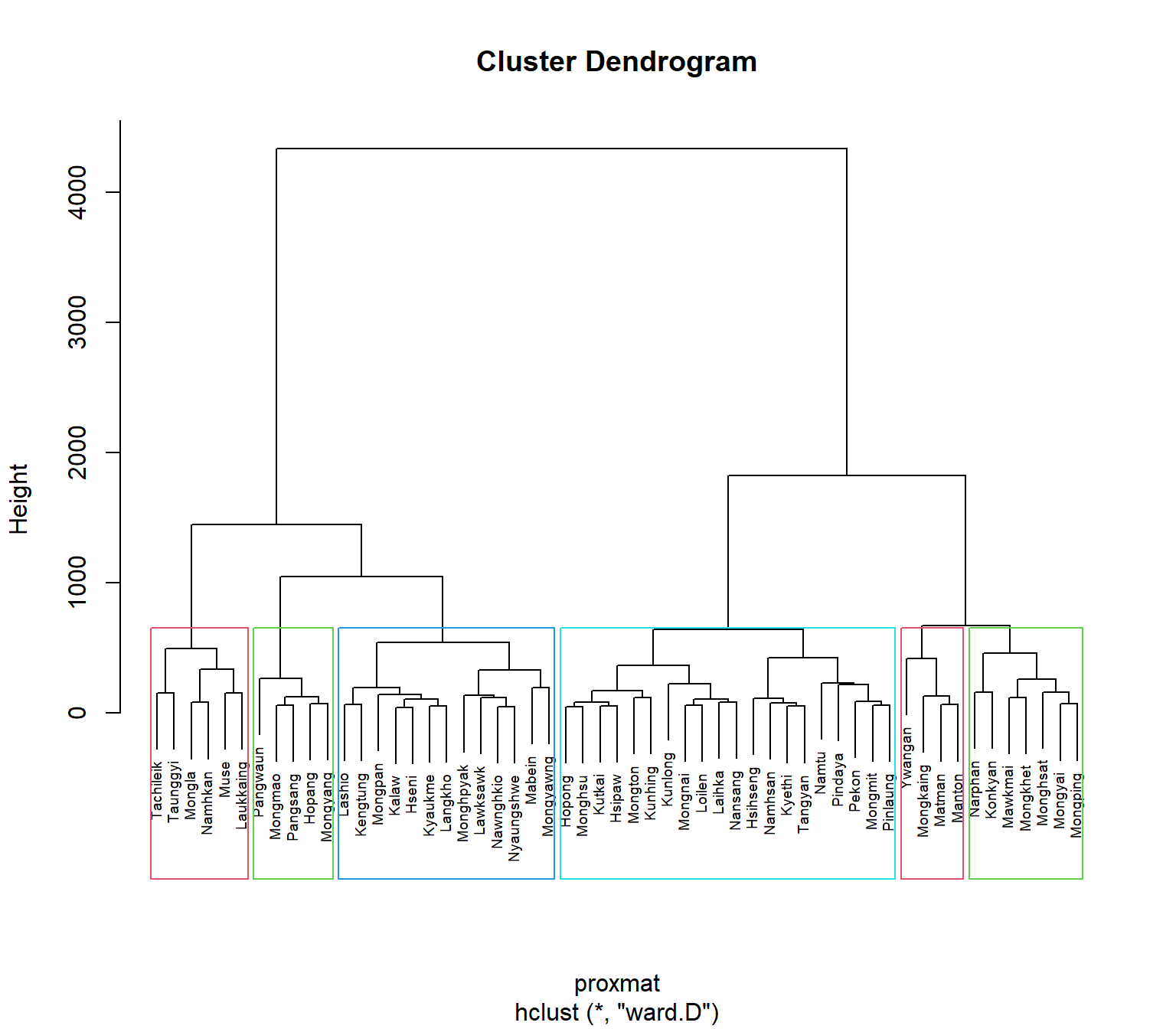
7.8 Visually-driven hierarchical clustering analysis
In this section, we will perform visually-driven hiearchical clustering analysis by using heatmaply package.
With heatmaply, we are able to build both highly interactive cluster heatmap or static cluster heatmap.
7.8.1 Transforming the data frame into a matrix
The data has to be a data matrix to make a heatmap using the heatmaply package.
The code chunk below will be used to transform shan_ict data frame into a data matrix.
shan_ict_mat <- data.matrix(shan_ict)7.8.2 Plotting the interactive cluster heatmap using heatmaply()
In the code chunk below, the heatmaply() of heatmaply package is used to build an interactive cluster heatmap.
heatmaply(normalize(shan_ict_mat),
Colv=NA,
dist_method = "euclidean",
hclust_method = "ward.D",
seriate = "OLO",
colors = Blues,
k_row = 6,
margins = c(NA,200,60,NA),
fontsize_row = 4,
fontsize_col = 5,
main="Geographic Segmentation of Shan State by ICT indicators",
xlab = "ICT Indicators",
ylab = "Townships of Shan State"
)7.9 Mapping the clusters formed
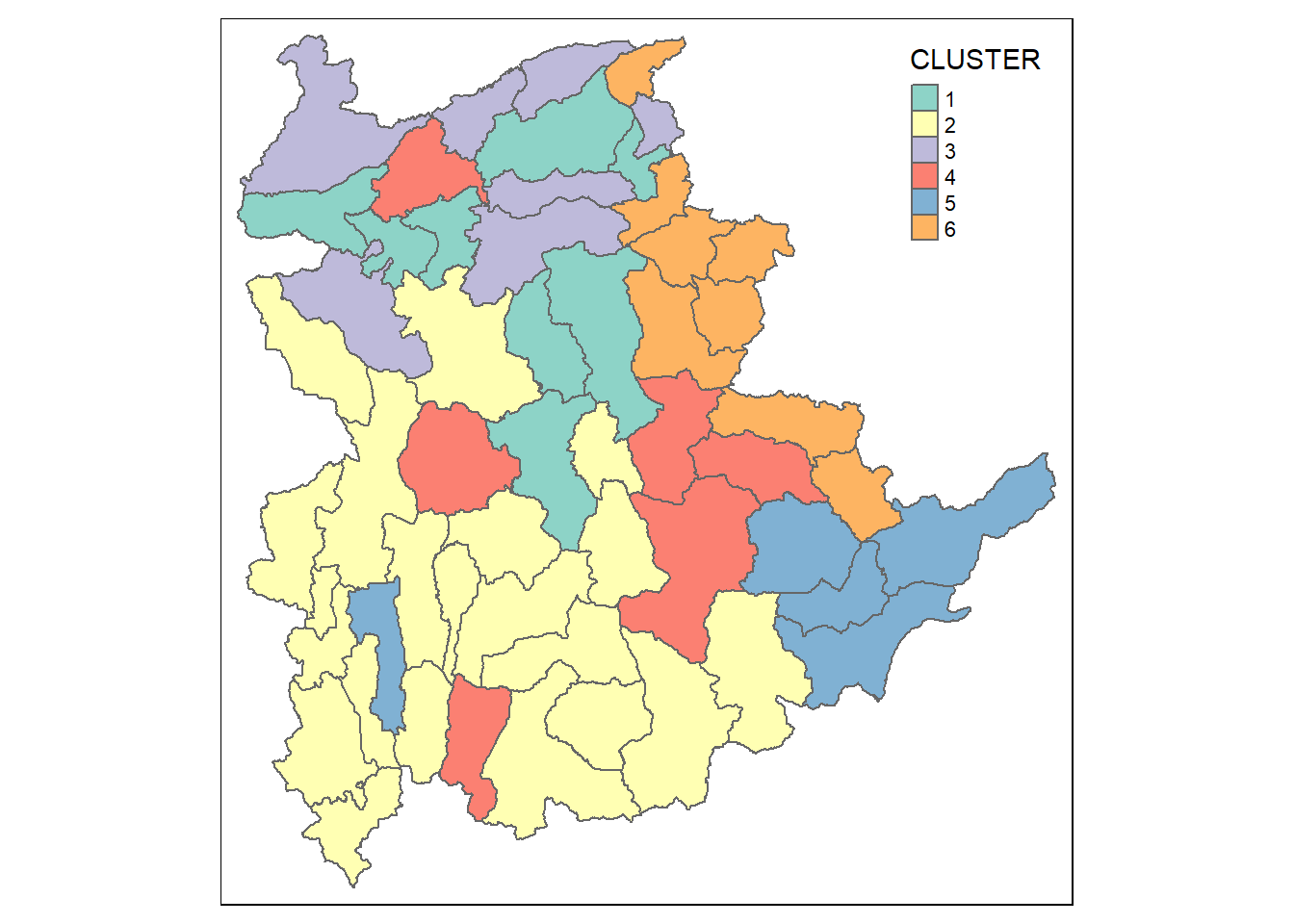
With closed examination of the dendragram above, we have decided to retain six clusters.
cutree() of R Base will be used in the code chunk below to derive a 6-cluster model.
groups <- as.factor(cutree(hclust_ward, k=6))The output is called groups which is a list object.
In order to visualise the clusters, the groups object need to be appended onto shan_sf simple feature object.
The code chunk below performs the following three steps:
the groups list object will be converted into a matrix using as.matrix();
cbind() is used to append groups matrix onto shan_sf to produce an output simple feature object called
shan_sf_cluster; andrename of dplyr package is used to rename as.matrix.groups field as CLUSTER.
shan_sf_cluster <- cbind(shan_sf, as.matrix(groups)) %>%
rename(`CLUSTER`=`as.matrix.groups.`)Next, qtm() of tmap package is used to plot the choropleth map to show the 6 clusters formed.
qtm(shan_sf_cluster, "CLUSTER")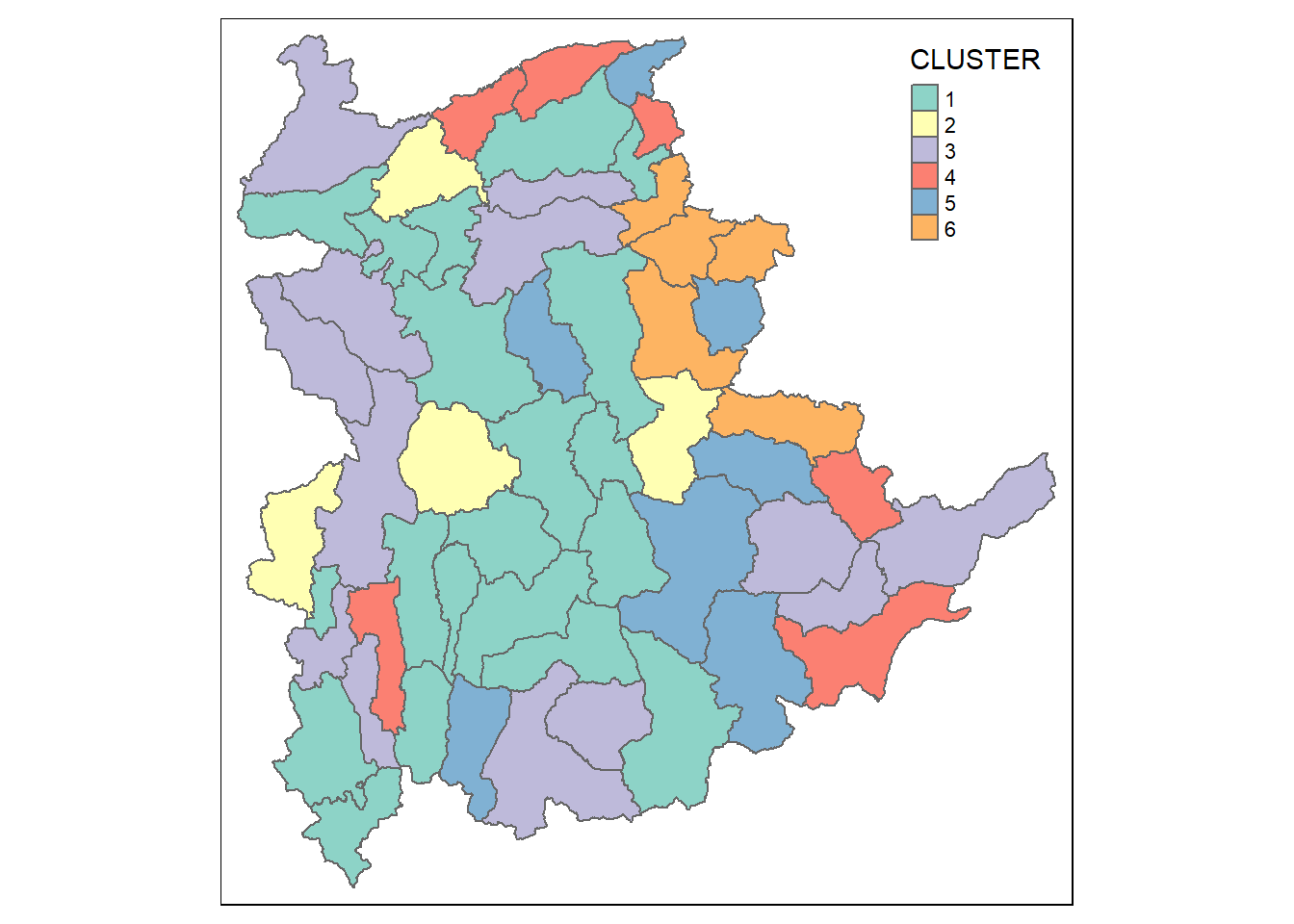
However, we can see that the clustered formed are very fragmented. The is one of the major limitations when non-spatial clustering algorithm such as hierarchical cluster analysis method is used.
8 Spatially Constrained Clustering - SKATER Approach
In this section, we will derive spatially constrained cluster by using skater() from spdep package.
8.1 Converting data into SpatialPolygonsDataFrame
First, we will need to convert shan_sf into a SpatialPolygonsDataFrame. This is because SKATER function only supports sp objects such as SpatialPolygonDataFrame.
The code chunk below uses as_Spatial() of sf package to convert shan_sf into a SpatialPolygonDataFrame called shan_sp.
shan_sp <- as_Spatial(shan_sf)8.2 Computing Neighbour List
Next, poly2nd() of spdep package will be used to compute the neighbours list from polygon list.
shan.nb <- poly2nb(shan_sp)
summary(shan.nb)Neighbour list object:
Number of regions: 55
Number of nonzero links: 264
Percentage nonzero weights: 8.727273
Average number of links: 4.8
Link number distribution:
2 3 4 5 6 7 8 9
5 9 7 21 4 3 5 1
5 least connected regions:
3 5 7 9 47 with 2 links
1 most connected region:
8 with 9 linksWe will plot the neighbours list in shan_sp by using the code chunk below. We will first plot the community area boundaries. It is important to first plot the area boundaries as the they extend further than the network graph. If done otherwise, some of the boundaries will be clipped. We then plot the neighbour list object, with coordinates applied to the original SpatialPolygonDataFrame (Shan state township boundaries) to extract the centroids of the polygons. These are used as the nodes for the graph representation. We also set the color to blue and specify add=TRUE to plot the network on top of the boundaries.
plot(shan_sp,
border=grey(.5))
plot(shan.nb,
coordinates(shan_sp),
col="blue",
add=TRUE)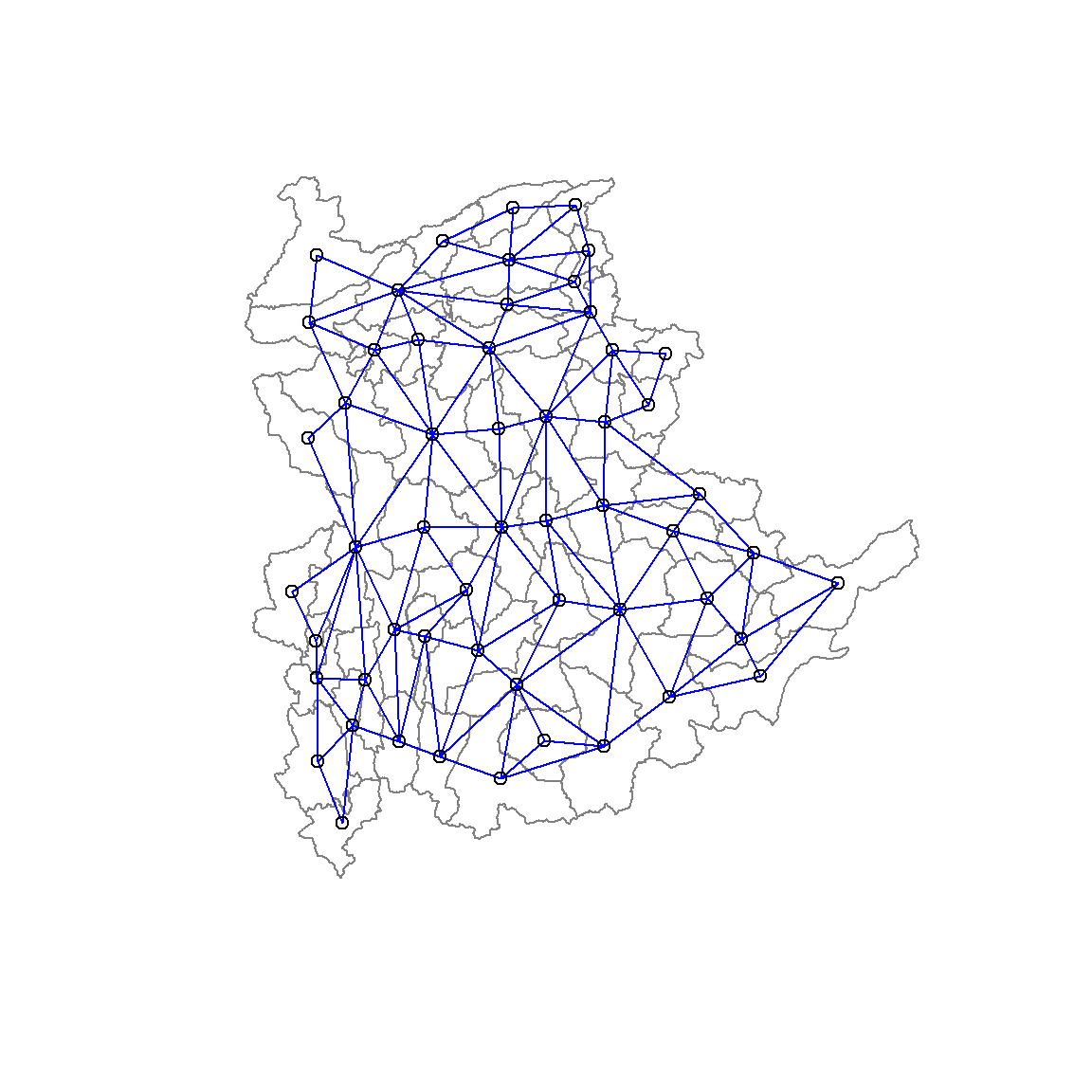
8.3 Computing minimum spanning tree
In this section, we will compute the minimum spanning tree. The minimum spanning tree is the one whose cumulative edge weights have the smallest value. We can think of this as the least cost path that goes through the entire graph and touches very node.
8.3.1 Calculating edge costs
Next, nbcosts() of spdep package is used to compute the cost of each edge. It is the distance between it nodes. This function compute this distance using a data.frame with observations vector in each node.
The code chunk below is used to compute the cost of each edge.
lcosts <- nbcosts(shan.nb, shan_ict)For each observation, lcosts this gives the pairwise dissimilarity between its values on the five variables and that of each of its neighbours. This forms the notion of a generalised weight for a spatial weights matrix.
Next, We will incorporate these costs into a weights object, i.e., we convert the neighbour list to a list weights object by specifying the just computed lcosts as the weights.
In order to achieve this, nb2listw() of spdep package is used as shown in the code chunk below.
We specify the style as B to make sure the cost values are not row-standardised.
shan.w <- nb2listw(shan.nb,
lcosts,
style="B")
summary(shan.w)Characteristics of weights list object:
Neighbour list object:
Number of regions: 55
Number of nonzero links: 264
Percentage nonzero weights: 8.727273
Average number of links: 4.8
Link number distribution:
2 3 4 5 6 7 8 9
5 9 7 21 4 3 5 1
5 least connected regions:
3 5 7 9 47 with 2 links
1 most connected region:
8 with 9 links
Weights style: B
Weights constants summary:
n nn S0 S1 S2
B 55 3025 76267.65 58260785 5220160048.3.2 Computing minimum spanning tree
Next, we will calculate the minimum spanning tree. The minimum spanning tree is computed by mean of the mstree() of spdep package as shown in the code chunk below.
shan.mst <- mstree(shan.w)After computing the MST, we can check its class and dimension by using the code chunks below.
class(shan.mst)[1] "mst" "matrix"dim(shan.mst)[1] 54 3We can observe that the dimension is 54 and not 55. This is because the minimum spanning tree consists on n-1 edges (links) in order to traverse all the nodes.
We can display the content of shan.mst by using head() as shown in the code chunk below.
head(shan.mst) [,1] [,2] [,3]
[1,] 31 25 229.44658
[2,] 25 10 163.95741
[3,] 10 1 144.02475
[4,] 10 9 157.04230
[5,] 9 8 90.82891
[6,] 8 6 140.01101The plot method for the MST include a way to show the observation numbers of the nodes in addition to the edge. As before, we plot this together with the township boundaries. We can see how the initial neighbour list is simplified to just one edge connecting each of the nodes, while passing through all the nodes.
plot(shan_sp, border=gray(.5))
plot.mst(shan.mst,
coordinates(shan_sp),
col="blue",
cex.lab=0.7,
cex.circles=0.005,
add=TRUE)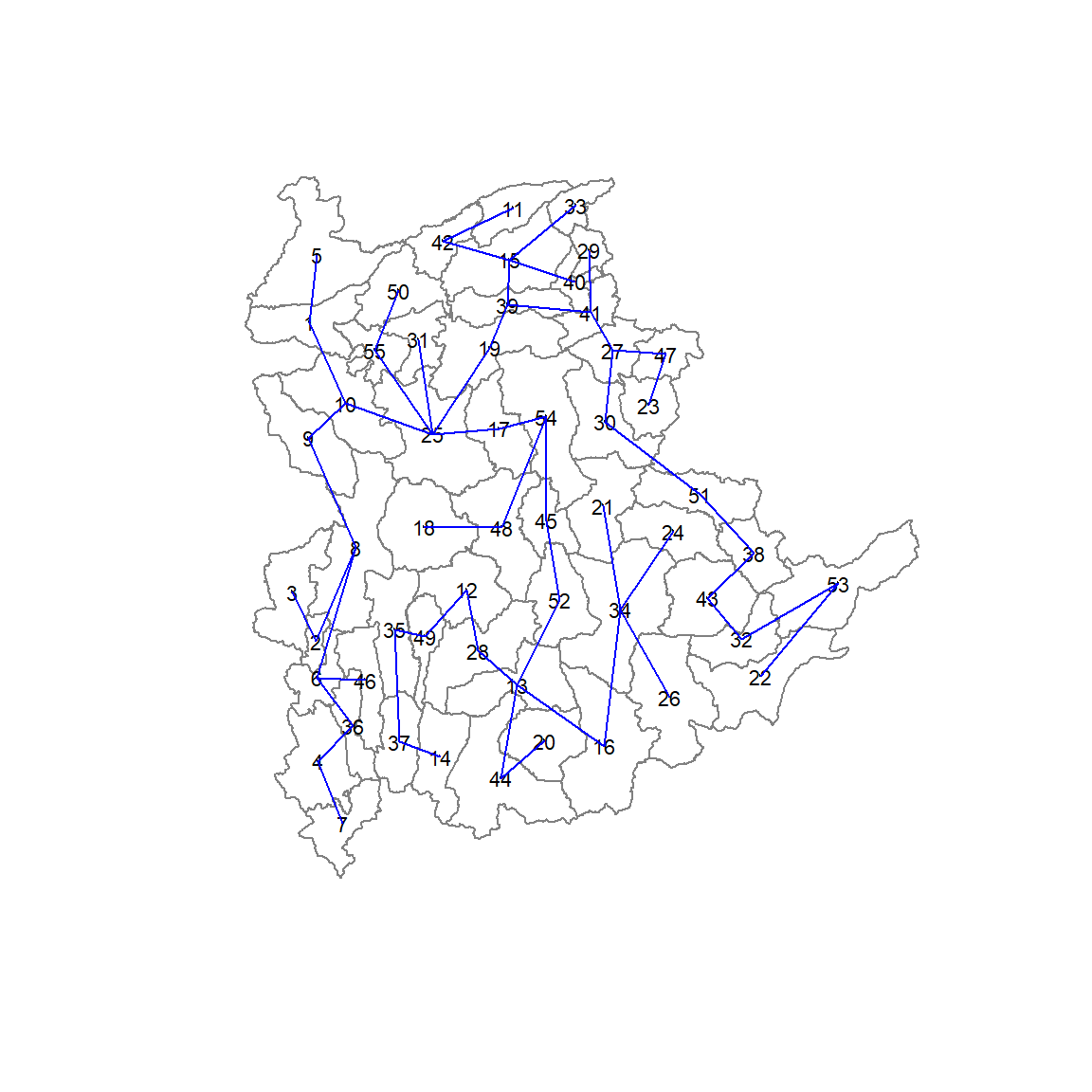
8.4 Computing spatially constrained clusters using SKATER method
The code chunk below computes the spatially constrained cluster using skater() of spdep package.
clust6 <- skater(edges = shan.mst[,1:2],
data = shan_ict,
method = "euclidean",
ncuts = 5)The skater() takes three mandatory arguments:
edges: the first two columns of the MST matrix (i.e. excluding the cost)
data: the data matrix (to update the costs as units are being grouped), and
ncuts: the number of cuts. Note: It is set to one less than the number of clusters.
The result of the skater() is an object of class skater. We can examine its contents by using the code chunk below.
str(clust6)List of 8
$ groups : num [1:55] 3 3 6 3 3 3 3 3 3 3 ...
$ edges.groups:List of 6
..$ :List of 3
.. ..$ node: num [1:22] 13 48 54 55 45 37 34 16 25 31 ...
.. ..$ edge: num [1:21, 1:3] 48 55 54 37 34 16 45 31 13 13 ...
.. ..$ ssw : num 3423
..$ :List of 3
.. ..$ node: num [1:18] 47 27 53 38 42 15 41 51 43 32 ...
.. ..$ edge: num [1:17, 1:3] 53 15 42 38 41 51 15 27 15 43 ...
.. ..$ ssw : num 3759
..$ :List of 3
.. ..$ node: num [1:11] 2 6 8 1 36 4 10 9 46 5 ...
.. ..$ edge: num [1:10, 1:3] 6 1 8 36 4 6 8 10 10 9 ...
.. ..$ ssw : num 1458
..$ :List of 3
.. ..$ node: num [1:2] 44 20
.. ..$ edge: num [1, 1:3] 44 20 95
.. ..$ ssw : num 95
..$ :List of 3
.. ..$ node: num 23
.. ..$ edge: num[0 , 1:3]
.. ..$ ssw : num 0
..$ :List of 3
.. ..$ node: num 3
.. ..$ edge: num[0 , 1:3]
.. ..$ ssw : num 0
$ not.prune : NULL
$ candidates : int [1:6] 1 2 3 4 5 6
$ ssto : num 12613
$ ssw : num [1:6] 12613 10977 9962 9540 9123 ...
$ crit : num [1:2] 1 Inf
$ vec.crit : num [1:55] 1 1 1 1 1 1 1 1 1 1 ...
- attr(*, "class")= chr "skater"The most interesting component of this list structure is the groups vector containing the labels of the cluster to which each observation belongs (as before, the label is arbitary). This is followed by a detailed summary for each of the clusters, provided in the edges.groups list. Sum of squares measures are given as ssto for the total and ssw to show the effect of each of the cuts on the overall criterion.
We can check the cluster assignment by using the code chunk below.
ccs6 <- clust6$groups
ccs6 [1] 3 3 6 3 3 3 3 3 3 3 2 1 1 1 2 1 1 1 2 4 1 2 5 1 1 1 2 1 2 2 1 2 2 1 1 3 1 2
[39] 2 2 2 2 2 4 1 3 2 1 1 1 2 1 2 1 1We can find out how many observations there are in each cluster by means of the table command. Parenthetially, we can also find this as the dimension of each vector in the lists contained in edges.groups. For example, the first list has node with dimension 22 (given by $ node: num [1:22]), which is also the number of observations in the first cluster ()which aligns with the results from the code chunk below).
table(ccs6)ccs6
1 2 3 4 5 6
22 18 11 2 1 1 Lastly, we can also plot the pruned tree that shows the five clusters on top of the townshop area.
plot(shan_sp, border=gray(.5))
plot(clust6,
coordinates(shan_sp),
cex.lab=.7,
groups.colors=c("red","green","blue", "brown", "pink"),
cex.circles=0.005,
add=TRUE)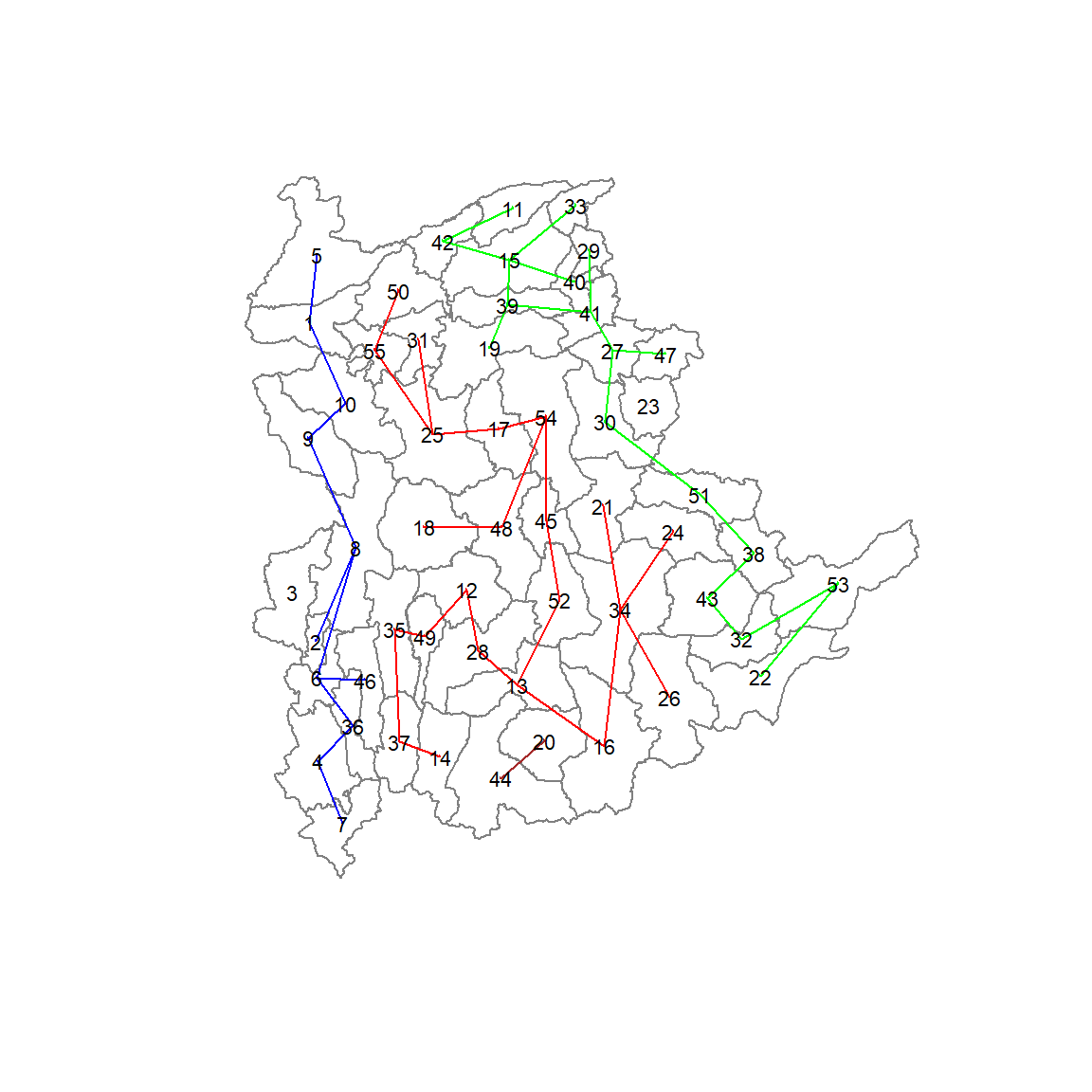
8.5 Visualising the clusters in a choropleth map
The code chunk below is used to plot the newly derived clusters by using SKATER method.
groups_mat <- as.matrix(clust6$groups)
shan_sf_spatialcluster <- cbind(shan_sf_cluster, as.factor(groups_mat)) %>%
rename(`SP_CLUSTER`=`as.factor.groups_mat.`)
qtm(shan_sf_spatialcluster, "SP_CLUSTER")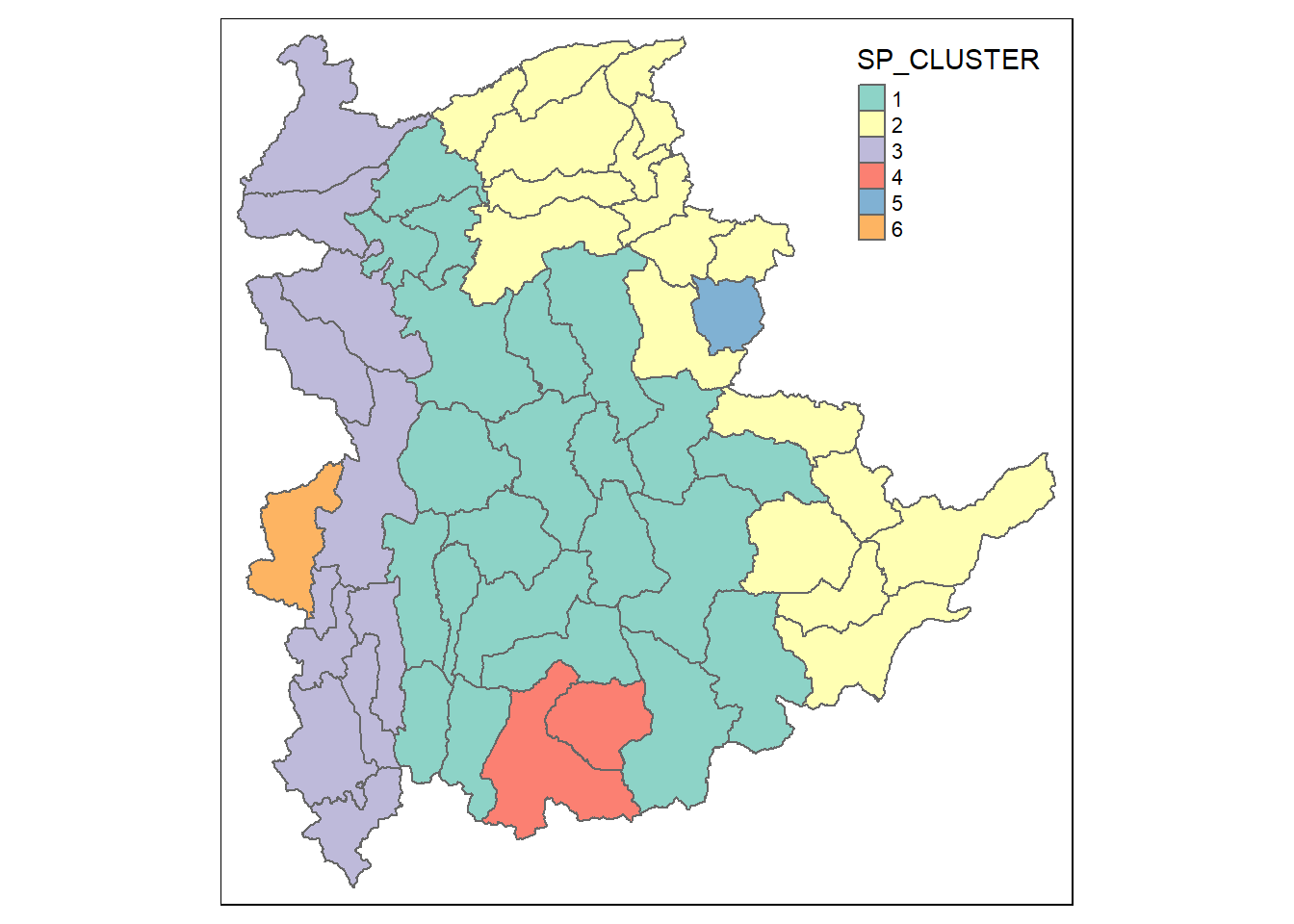
For easy comparison, it is better to place both the hierarchical clustering and spatially constrained hierarchical clustering maps next to each other.
hclust.map <- qtm(shan_sf_cluster,
"CLUSTER") +
tm_borders(alpha = 0.5)
shclust.map <- qtm(shan_sf_spatialcluster,
"SP_CLUSTER") +
tm_borders(alpha = 0.5)
tmap_arrange(hclust.map, shclust.map,
asp=NA, ncol=2)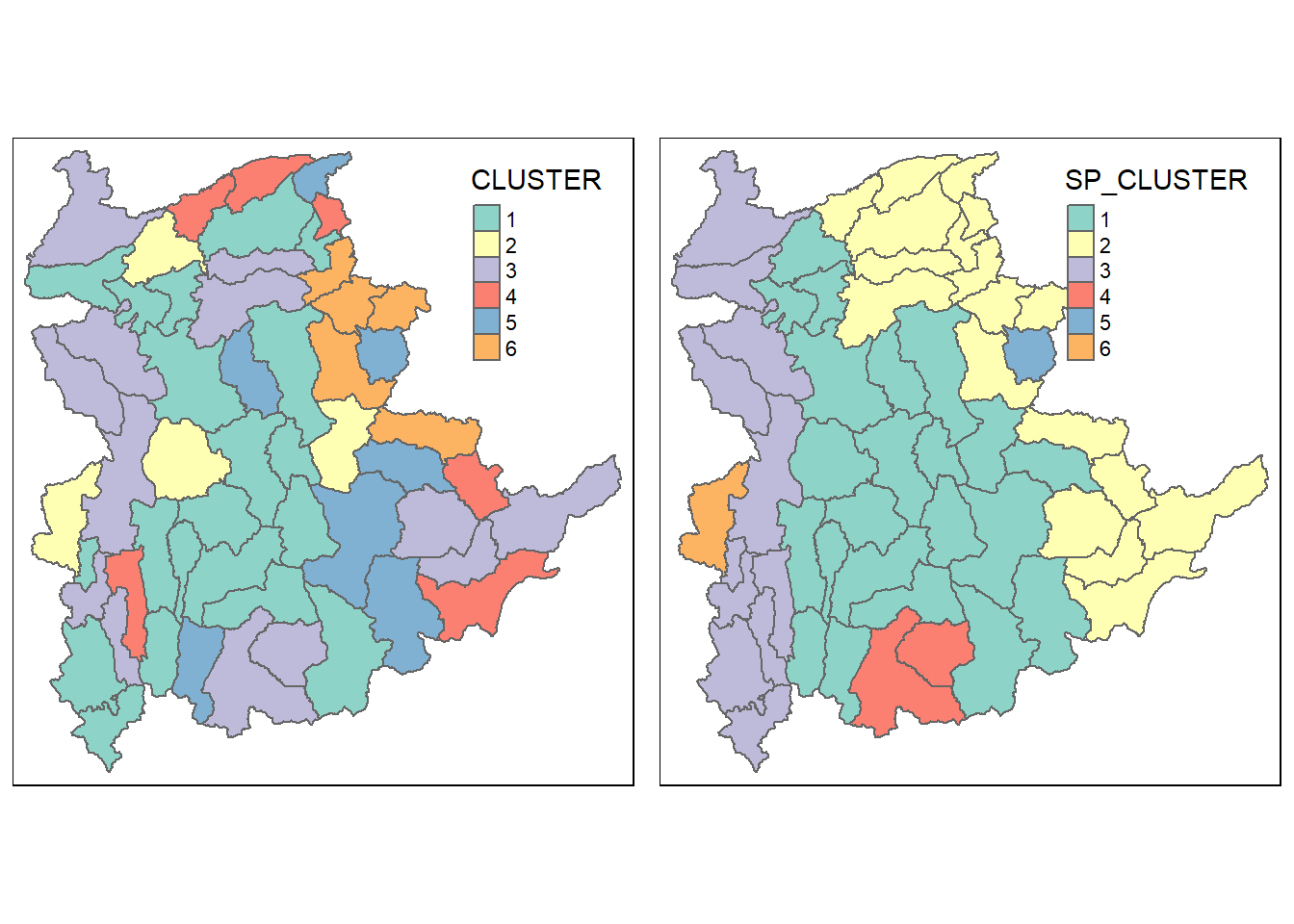
Comparing these 2 maps, it is clear that the spatially constrained clustering gives a better clustering where clusters are constrained together and not fragmented, unlike in the map given by hierarchical clustering.
9 Spatially Constrained Clustering: ClustGeo Method
In this section, we will use functions provided in ClustGeo package to perform non-spatially constrained hierarchical cluster analysis and spatially constrained cluster analysis.
9.1 Ward-like hierarchical clustering: ClustGeo
ClustGeo package provides function called hclustgeo() to perform a typical Ward-like hierarchical clustering just like hclust() used in the previous section.
To perform non-spatially constrained hierarchical clustering, we only need to provide a dissimilarity matrix to the function as shown in the code chunk below.
nongeo_cluster <- hclustgeo(proxmat)
plot(nongeo_cluster, cex = 0.5)
rect.hclust(nongeo_cluster,
k = 6,
border = 2:5)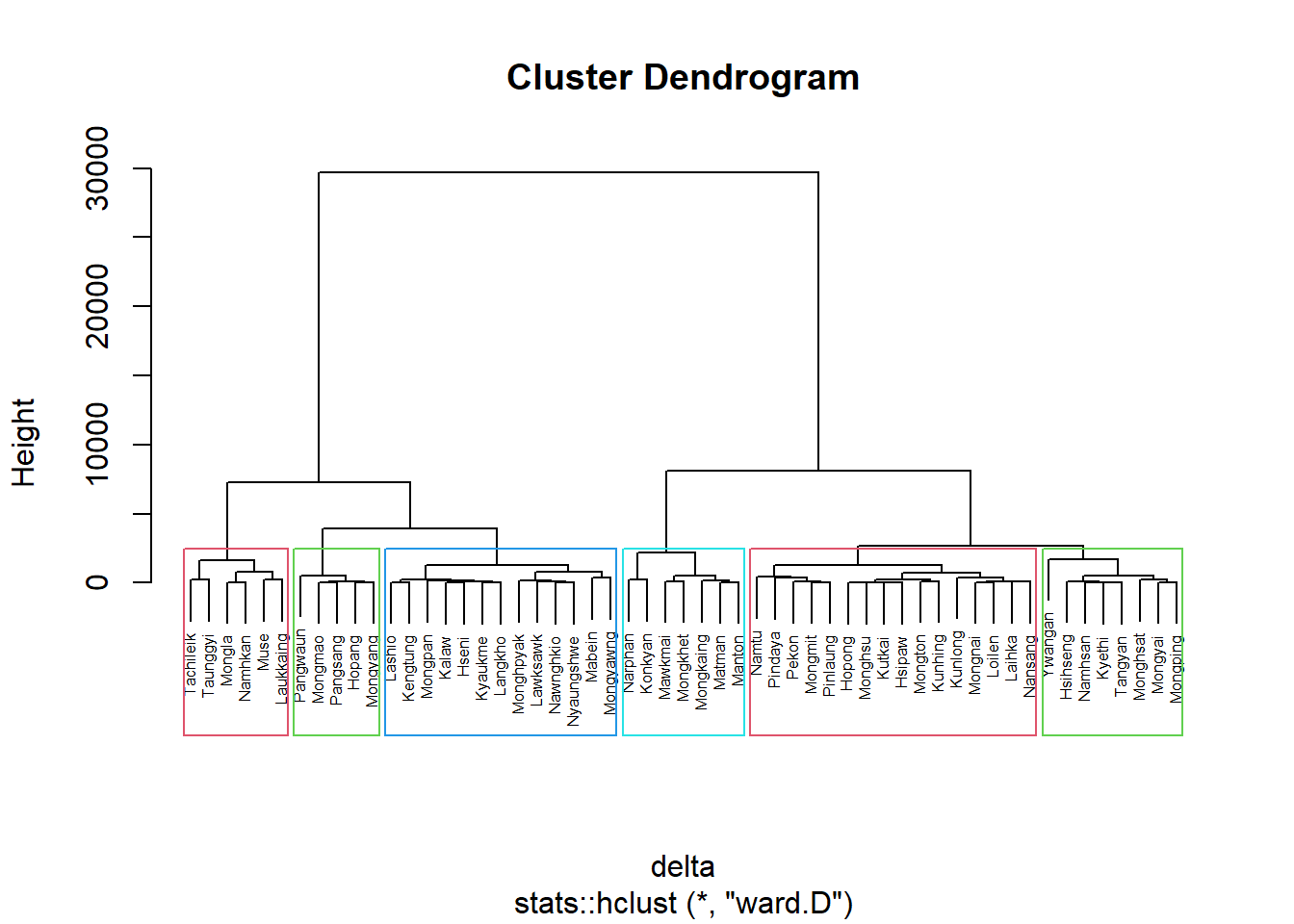
Note that the dissimilarity matrix must be an object of class dist, i.e. an object obtained with the function dist().
9.1.1 Mapping the clusters formed
Similarly, we can plot the clusters on a categorical area shaded map by using the steps in 7.9 Mapping the clusters formed.
groups <- as.factor(cutree(nongeo_cluster, k=6))shan_sf_ngeo_cluster <- cbind(shan_sf, as.matrix(groups)) %>%
rename(`CLUSTER` = `as.matrix.groups.`)qtm(shan_sf_ngeo_cluster, "CLUSTER")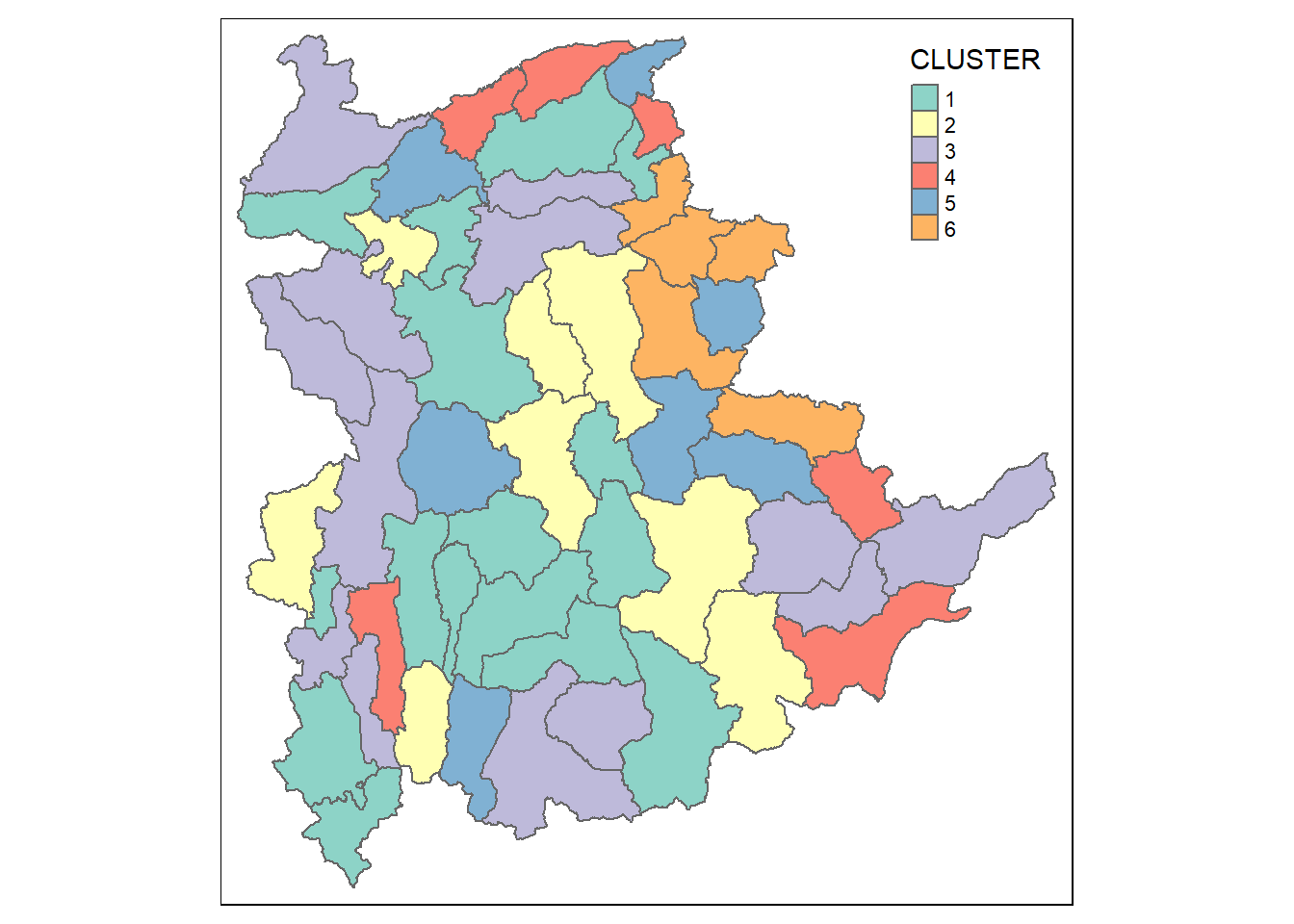
9.2 Spatially Constrained Hierarchical Clustering
Before we perform spatially constrained hierarchical clustering, a spatial distance matrix will be derived by using st_distance() of sf package.
dist <- st_distance(shan_sf, shan_sf)
distmat <- as.dist(dist)Notice that as.dist() is used to convert the data frame into matrix.
Next, choicealpha() will be used to determine a suitable value for the mixing parameter alpha as shown in the code chunk below. It uses both d0 distance (attribute homogeneity used in hierarchical clustering) as well as d1 contiguity matrix (spatial homogeneity). In hierarchical clustering, alpha value is 0 which is why only attribute space is considered and no spatial relationship is considered. Alpha value ranges from 0 to 1. At alpha = 1, only spatial homogeneity is considered (no consideration is given to attribute homogeneity).
In the following, we define the incremental value for alpha to be evaluated is 0.1.
cr <- choicealpha(proxmat, distmat, range.alpha = seq(0, 1, 0.1), K=6, graph = TRUE)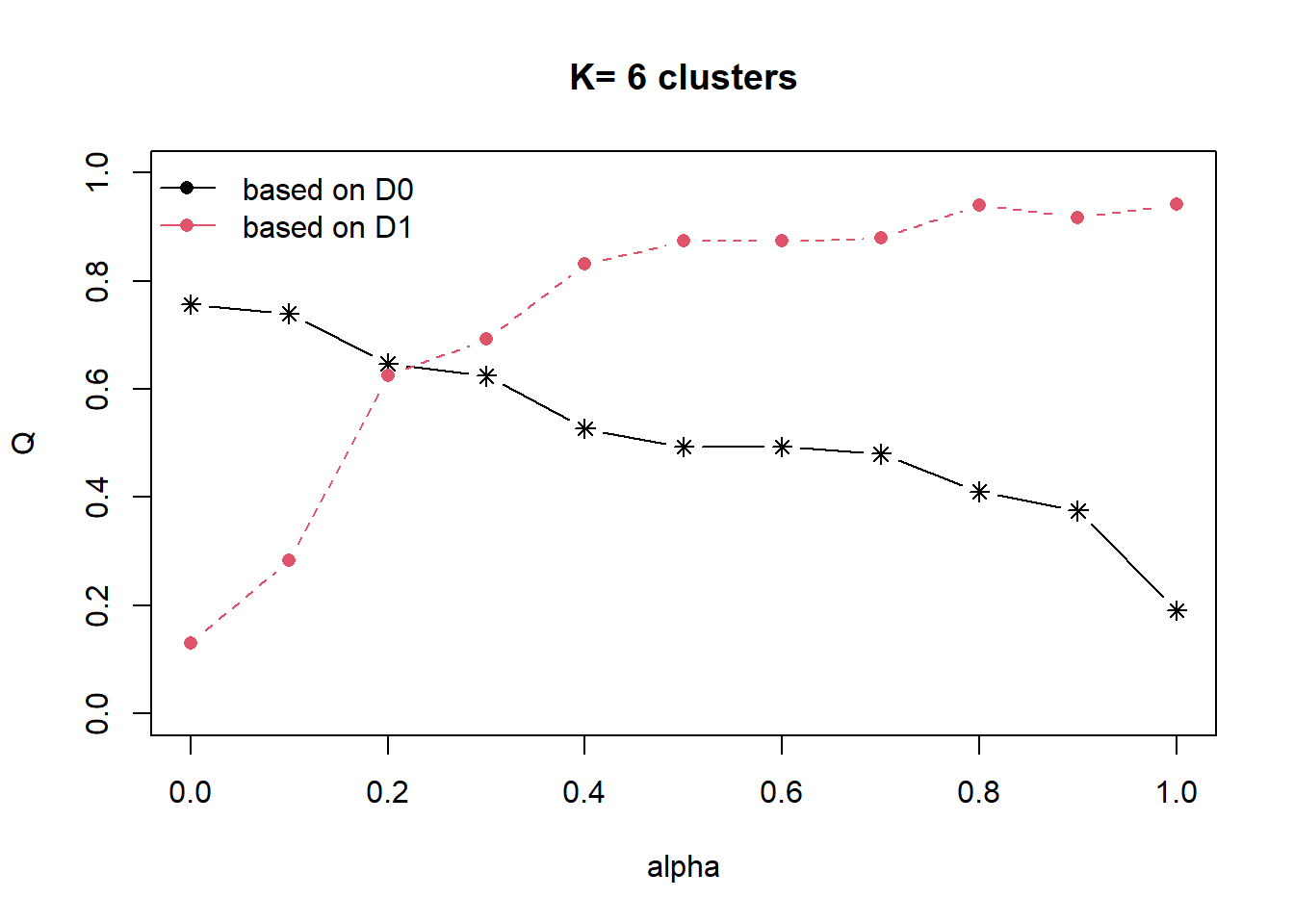
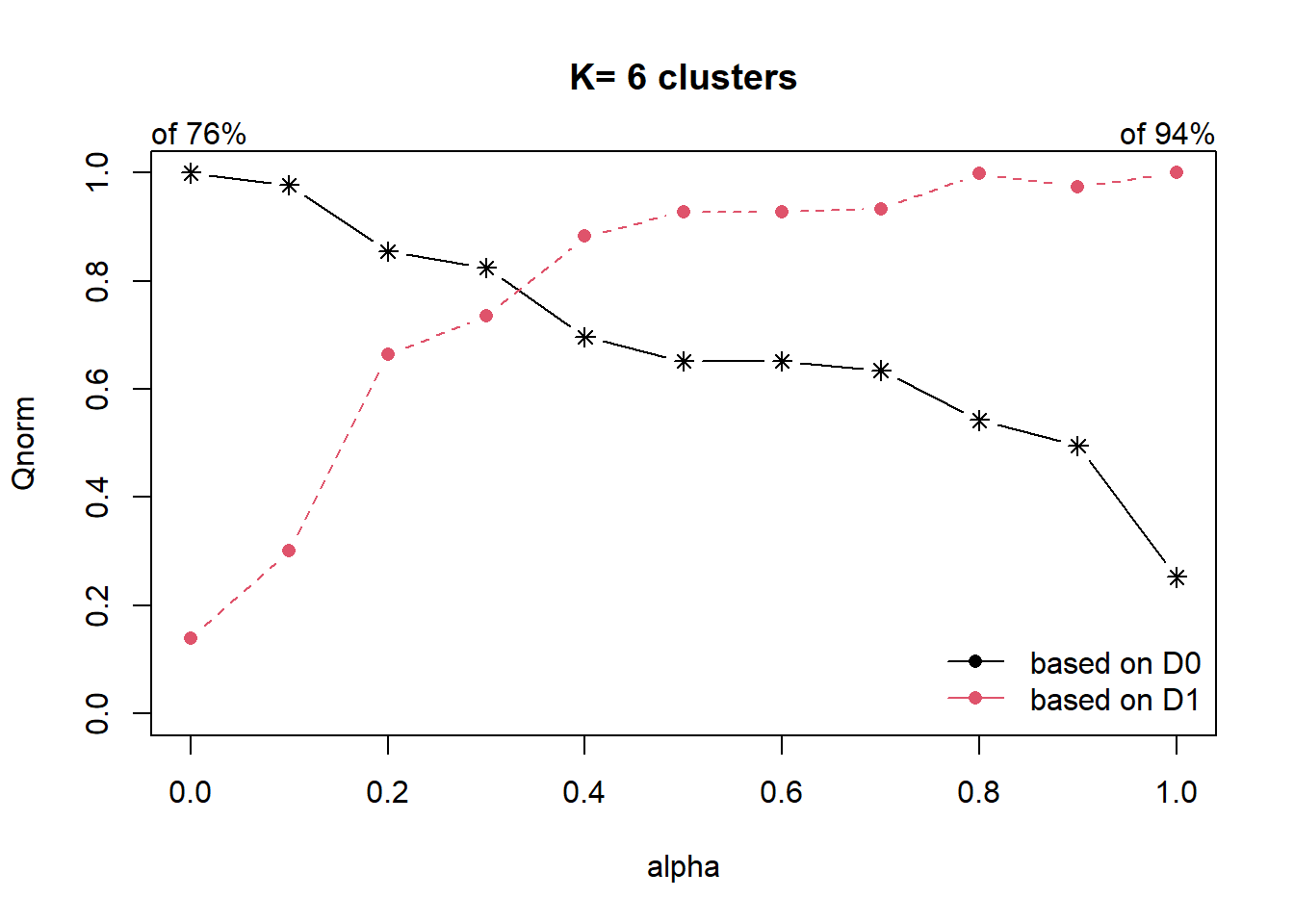
Two plots are given, the first graph shows the non-normalised result and the second graph shows the normalised result. The normalised graph should be used when there is significant difference in the range of values (for attribute distance and spatial relationship).
We can see that when we increase the value of alpha, the black line decreases - implying that the attribute homogeneity is being compromised.
We can also see that as we increase the alpha value from 0.1 to 0.2, the spatial homogeneity increases significantly from 0.3 to 0.6. Even as we increase the alpha value to 0.3, we only compromise the attribute homogeneity slightly as we continue to improve on spatial homogeneity.
With reference to the graphs above, alpha = 0.3 will be used as shown in the code chunk below.
clustG <- hclustgeo(proxmat, distmat, alpha = 0.3)Next, cutree() is used to derive the cluster object.
groups <- as.factor(cutree(clustG, k=6))We will then join back the group list with shan_sf polygon feature data frame by using the code chunk below.
shan_sf_Gcluster <- cbind(shan_sf, as.matrix(groups)) %>%
rename(`CLUSTER` = `as.matrix.groups.`)We can not plot the map of the newly delineated spatially constrained clusters.
qtm(shan_sf_Gcluster, "CLUSTER")